Question

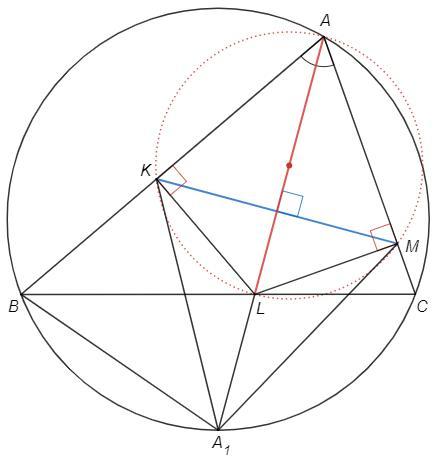
Биссектриса AL пересекает описанную окружность треугольника ABC в точке A1, K и M — основания перпендикуляров, опущенных из L на AB и AC. Докажите, что четырехугольник AKA1M равновелик треугольнику ABC.

Answer 1

Отрезок AL виден из точек K и M под прямым углом - точки K и M лежат на окружности диаметром AL.

AL - биссектриса ∠A. Диаметр AL проходит через середину дуги KM, следовательно перпендикулярен хорде KM.

S(AKA1M) =1/2 AA1*KM

S(ABC) =1/2 AB*AC*sinA

KM/sinA =AL (теорема синусов для △KAM) => KM =AL*sinA

∠AA1B=∠ACB (опираются на дугу AB) => △AA1B~△ACL (по двум углам)

AA1/AC=AB/AL => AA1*AL=AB*AC =>

1/2 AA1*AL*sinA =1/2 AB*AC*sinA => S(AKA1M) =S(ABC).