Предмет: Математика,
автор: fedcenkoana875
ПОЖАЛУЙСТА . 50 БАЛЛОВ
Приложения:
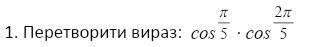
Ответы
Автор ответа:
0
Ответ:
Автор ответа:
0
Ответ:
Пошаговое объяснение:
cos π/5 ·cos (2π)/5=(2sin π/5 ·cos π/5 ·cos (2π)/5)/(2sin π/5)=(sin (2π)/5 ·cos (2π)/5)/(2cos π/5)=(sin72° ·cos72°)/(2cos36°)=(sin144°)/(4cos36°)=(cos36°)/(4cos36°)=1/4
Похожие вопросы
Предмет: Английский язык,
автор: Yomo
Предмет: Математика,
автор: FFFG849
Предмет: Другие предметы,
автор: Ranger98
Предмет: Математика,
автор: daryabozhko2006
Предмет: Окружающий мир,
автор: сашакоте1