Предмет: Математика,
автор: cda32
Срочнооооооооо
Пожалуйста
Приложения:

Ответы
Автор ответа:
1
Ответ:
1.
а
б
в
n принадлежит Z.
2.
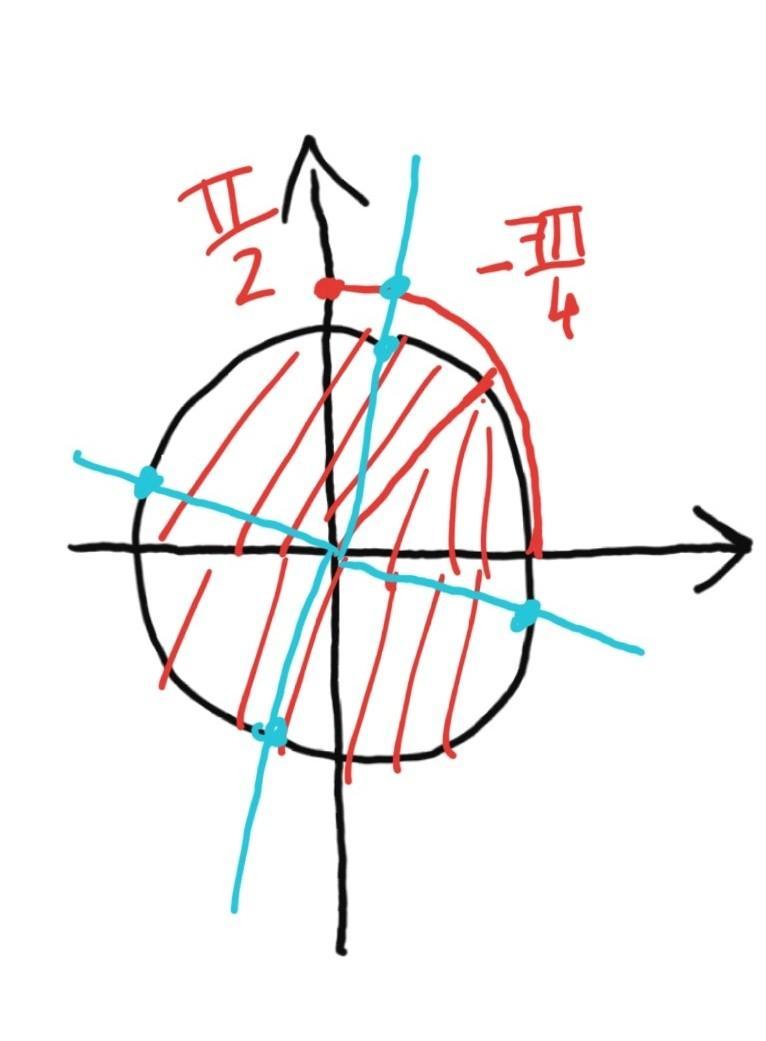
рисунок
Ответ: 5 корней
3.
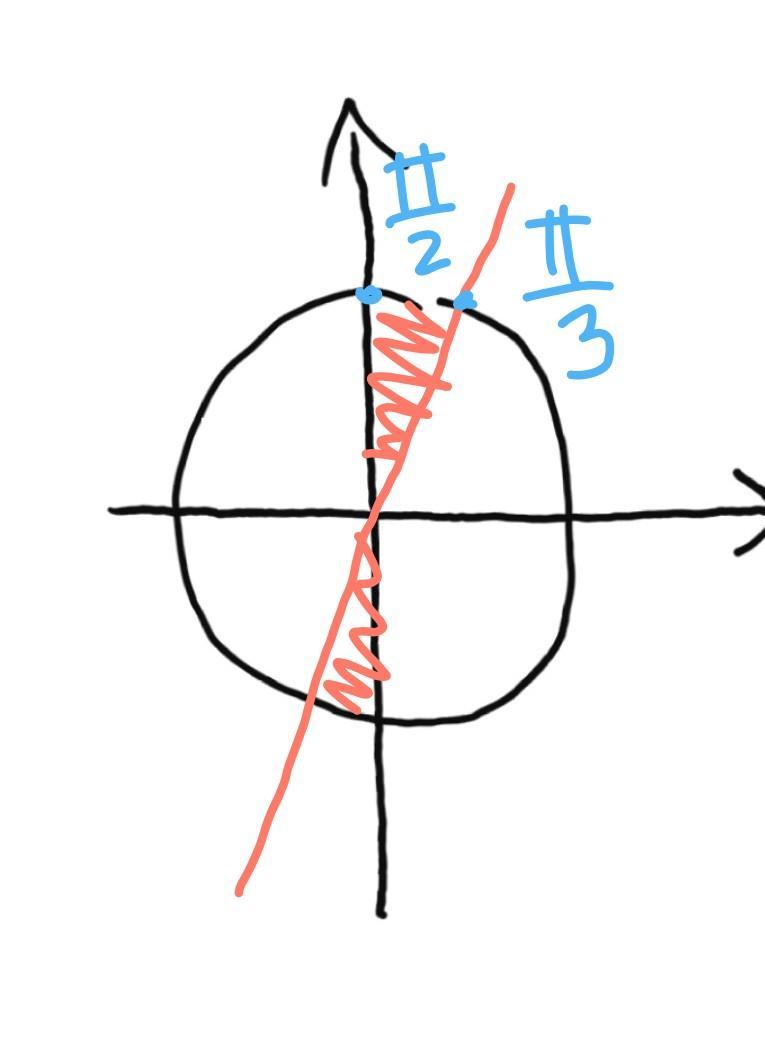
рисунок 2
n принадлежит Z.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: shogunuz
Предмет: Математика,
автор: tigrlena
Предмет: Русский язык,
автор: lkoplenko
Предмет: Русский язык,
автор: Аноним
Предмет: Обществознание,
автор: лубофь
(P.S хочу родить от тебя зазаза)