Question

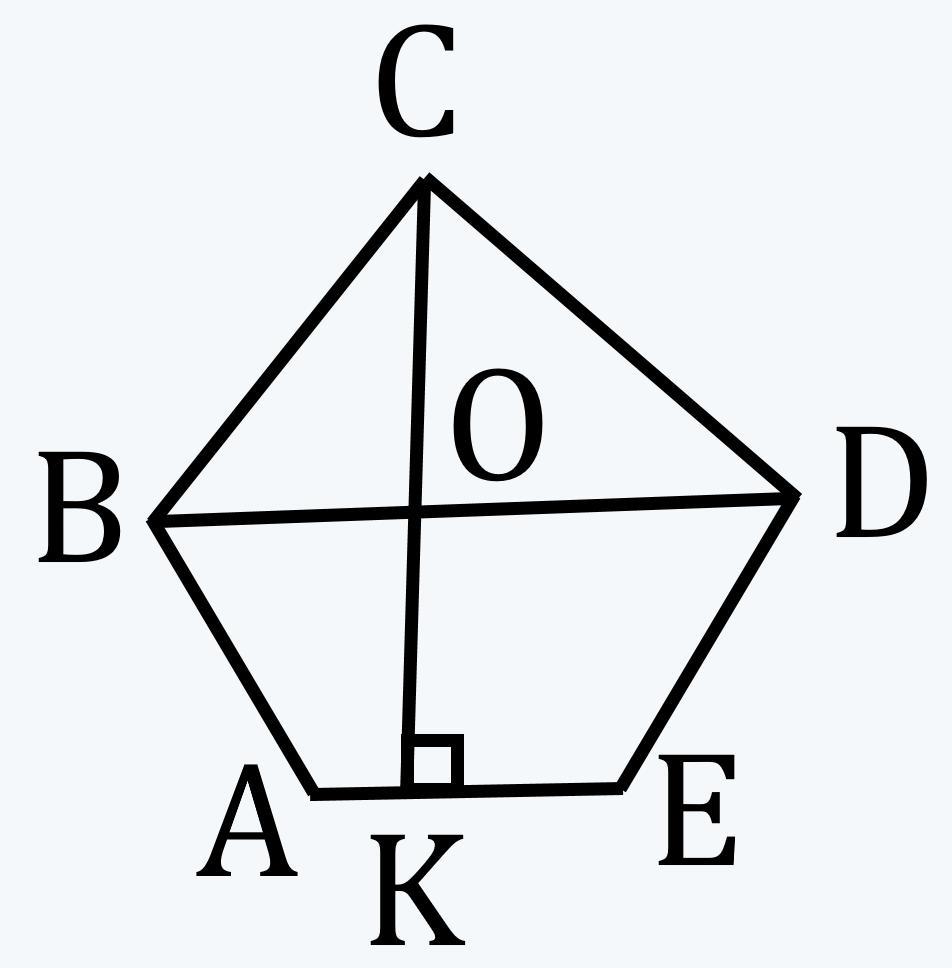
Найти площадь пятиугольника ABCDE, если BD║AE, CK ⊥ AE, BD=8см, AE=6см, CK=9см и CO=3см

Answer 1

Ответ:

54 $cm^{2}$

Пошаговое объяснение:

Площадь пятиугольника найдём как сумму площадей треугольника BCD и четырёхугольника ABDE.

1) Так как BD║AE, CK ⊥ AE, то  CО ⊥ BD, значит CО - высота треугольника BCD . Тогда площадь треугольника BCD найдём по формуле:

s = $\frac{1}{2}$ah

S = $\frac{1}{2}$·BD·CO = $\frac{1}{2}$·8·3= 12 см²

2) Четырехугольник ABDE - трапеция, так кк по условию BD║AE

Значит, S  = $\frac{1}{2}$·( BD + AE)·OK

OK - высота трапеции и равна СК - СО

ОК = 9 - 3 = 6 см.

Значит, S  = $\frac{1}{2}$·( 8 + 6)·6 = 42 см²

3) Искомая площадь будет равна S = 12 + 42 = 54 см²