Question

График какой функции можно построить, переместив график основной функции вниз и вправо?
1) Ни одной из данных
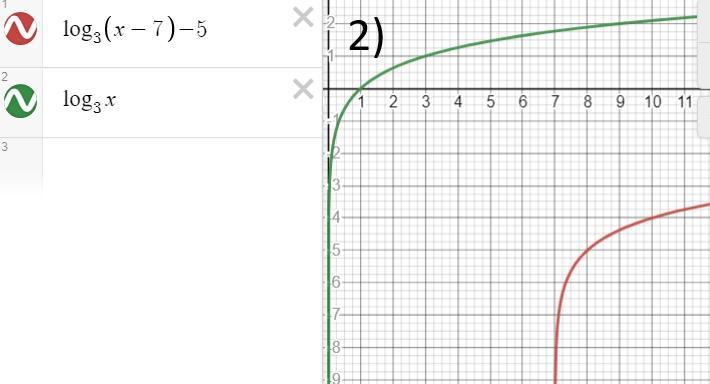
2) y=log3(x−7)−5
3) y=|x+7|−5
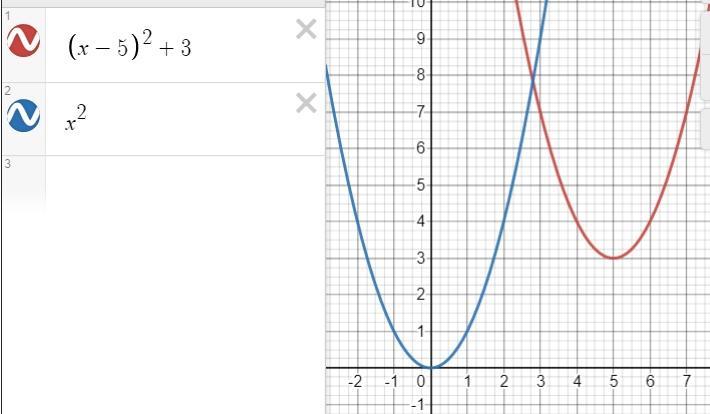
4) y=(x−5)2+3

Answer 1

Ответ:

переместив график основной функции вниз и вправо можно построить график функции  y = log₃(x−7)−5

Объяснение:

Если к ФУНКЦИИ  добавляется константа ( f(x) ± b ), то происходит сдвиг (параллельный перенос) её графика вдоль оси OY (вниз или вверх).

• чтобы построить график функции f(x) -b , нужно график f(x)   сдвинуть вдоль  оси OY  на b единиц вниз.

Если к АРГУМЕНТУ функции  добавляется константа  (  f(x±h) ), то происходит сдвиг (параллельный перенос) графика вдоль оси  ОХ.

• чтобы построить график функции f(x-h) , нужно график f(x) сдвинуть вдоль  оси ОХ  на h единиц вправо.

Сжатие или растяжение графика происходит при наличии коэффициента при АРГУМЕНТЕ ( f(kx) )

Разберем наши примеры.

2) y = log₃(x−7)−5  это функция вида f(x-h)-b, она строится путем параллельного переноса графика функции y=log₃(x) на 7 единиц вправо и на 5 единиц вниз.

3) y=|x+7|−5 это функция вида f(x-h)-b, она строится путем параллельного переноса графика функции y=|x| на 7 единиц влево и на 5 единиц вниз.

4) y=(x−5)²+3  то функция вида f(x-h)+b, она строится путем параллельного переноса графика функции y=х² на 5 единиц вправо и на 3 единицы вверх.