Предмет: Алгебра,
автор: kskksjxnsj
ПОМОГИТЕ ПОЖАЛУЙСТА, 2 и 4
Приложения:
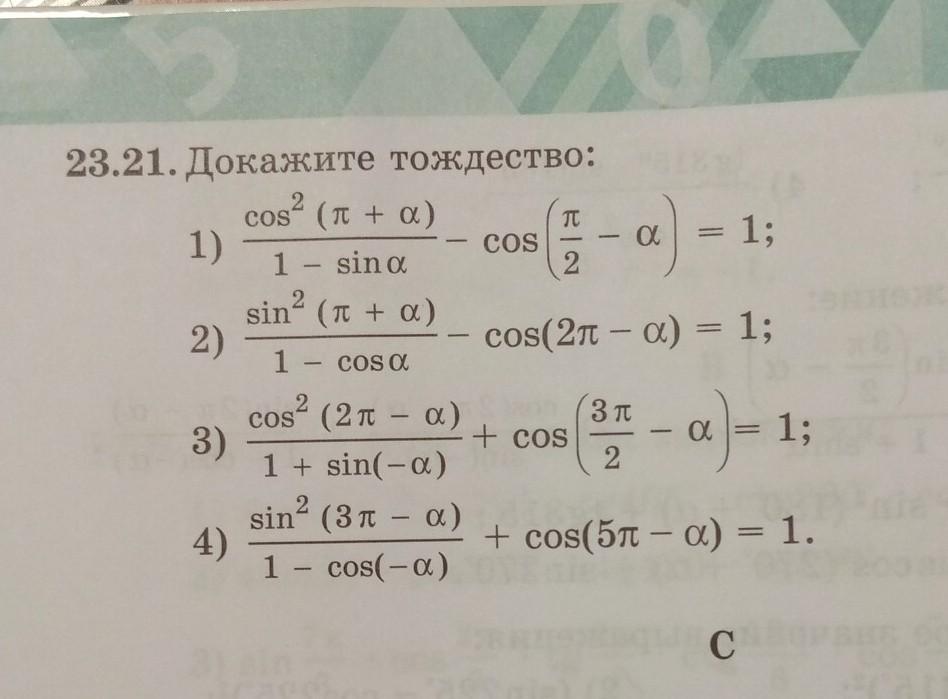
Ответы
Автор ответа:
1
Ответ:
2.
4.
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: 1963Oleg
Предмет: Математика,
автор: ЖенаМишиКоллинза
Предмет: Математика,
автор: lancelololo56
Предмет: Геометрия,
автор: Oleksiy2280