Предмет: Математика,
автор: noname281206
В треугольнике ABC AC = BC, AB = 6, tg A =12/5
Найдите АС
Ответы
Автор ответа:
6
Ответ:
AC= 7,8 ед.
Пошаговое объяснение:
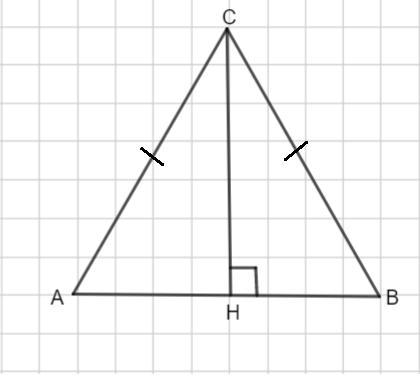
Рассмотрим Δ АВС - равнобедренный, так как АС=ВС.
АВ= 6 ед.
Проведем высоту СН. В равнобедренном треугольнике высота, проведенная к основанию является медианой.
Значит, АН=НВ = 6:2=3 ед.
По условию
Рассмотрим Δ АHС - прямоугольный.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Найдем АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: УченикЛадушка7
Предмет: Алгебра,
автор: prudkovanatali
Предмет: Математика,
автор: 79206017201
Предмет: Математика,
автор: Sergey3361