Предмет: Алгебра,
автор: alistochek
Как решить? (4sin^4 x - 1)корень -cosx=0 [pi/5pi/2]
Ответы
Автор ответа:
5
Ответ:
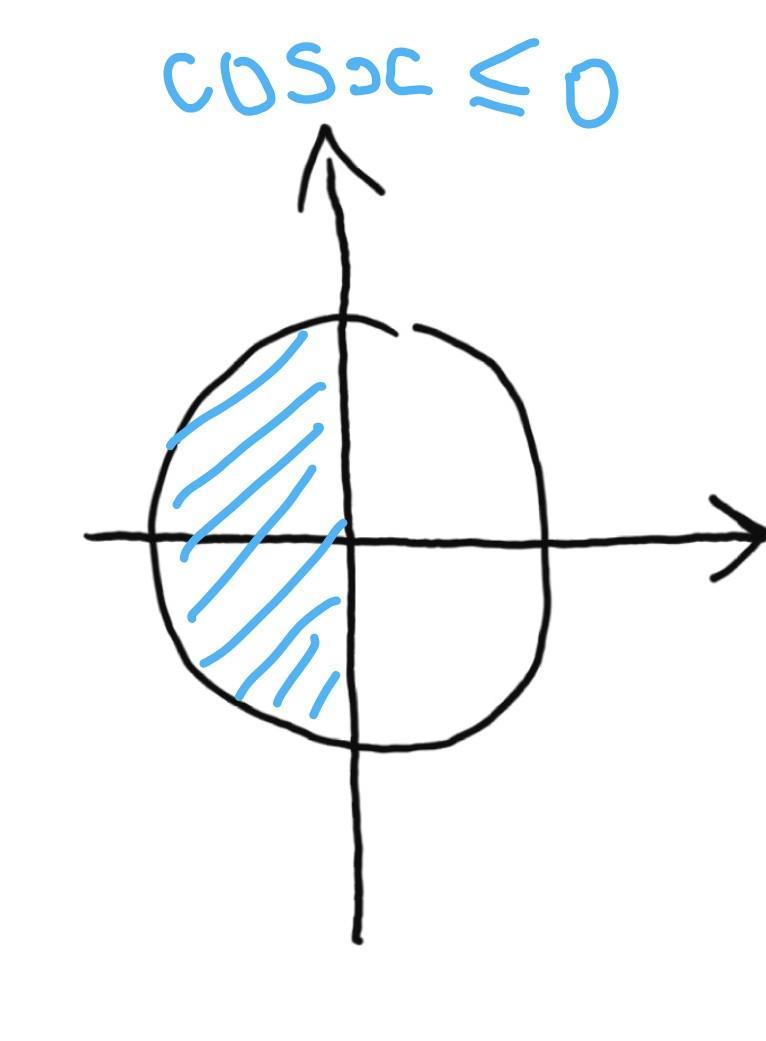
ОДЗ:
рисунок1
Все полученные корни должны входить в эту область.
n принадлежит Z.
n принадлежит Z.
корни х2 и х4 не входят в ОДЗ, поэтому их исключаем.
В итоге получаем:
б)
на промежутке:
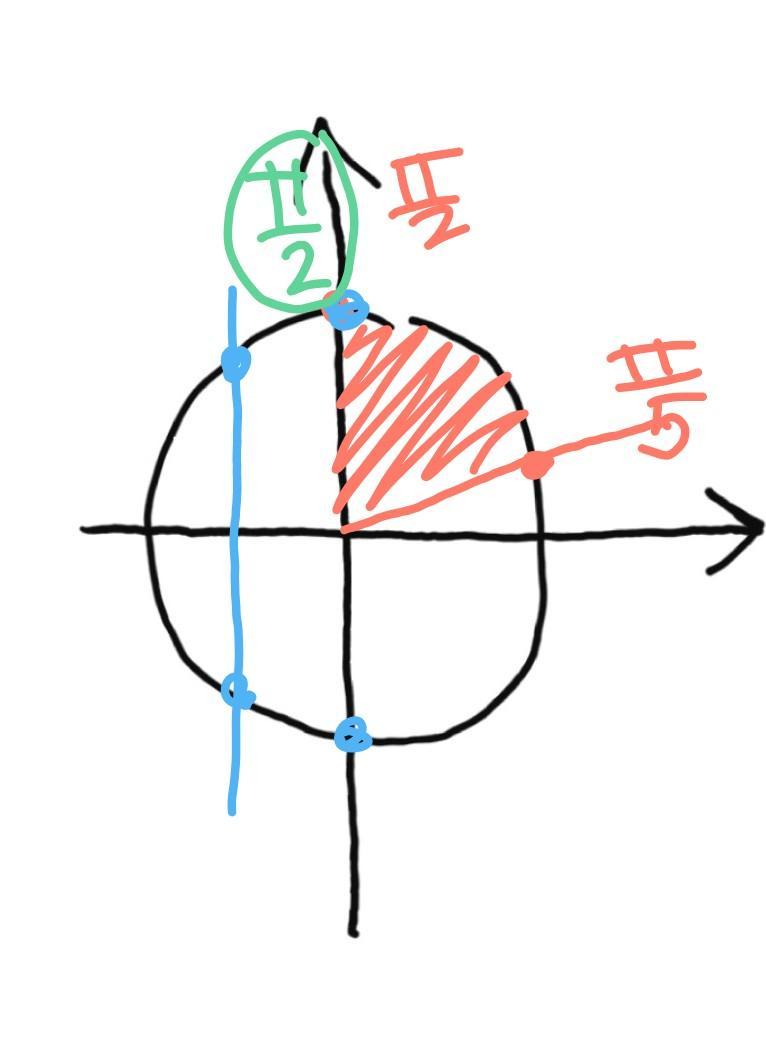
рисунок 2
красным заданы границы промежутка
синим отмечены все полученные корни
зеленым тот корень, что входит в промежуток.
входит только корень П/2
Ответ:
n принадлежит Z.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Areteas
Предмет: Алгебра,
автор: Areteas
Предмет: Русский язык,
автор: МишаHTS
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Zero3339