Предмет: Математика,
автор: Аноним
Сделайте уравнения пожалуйста уравнения
Приложения:
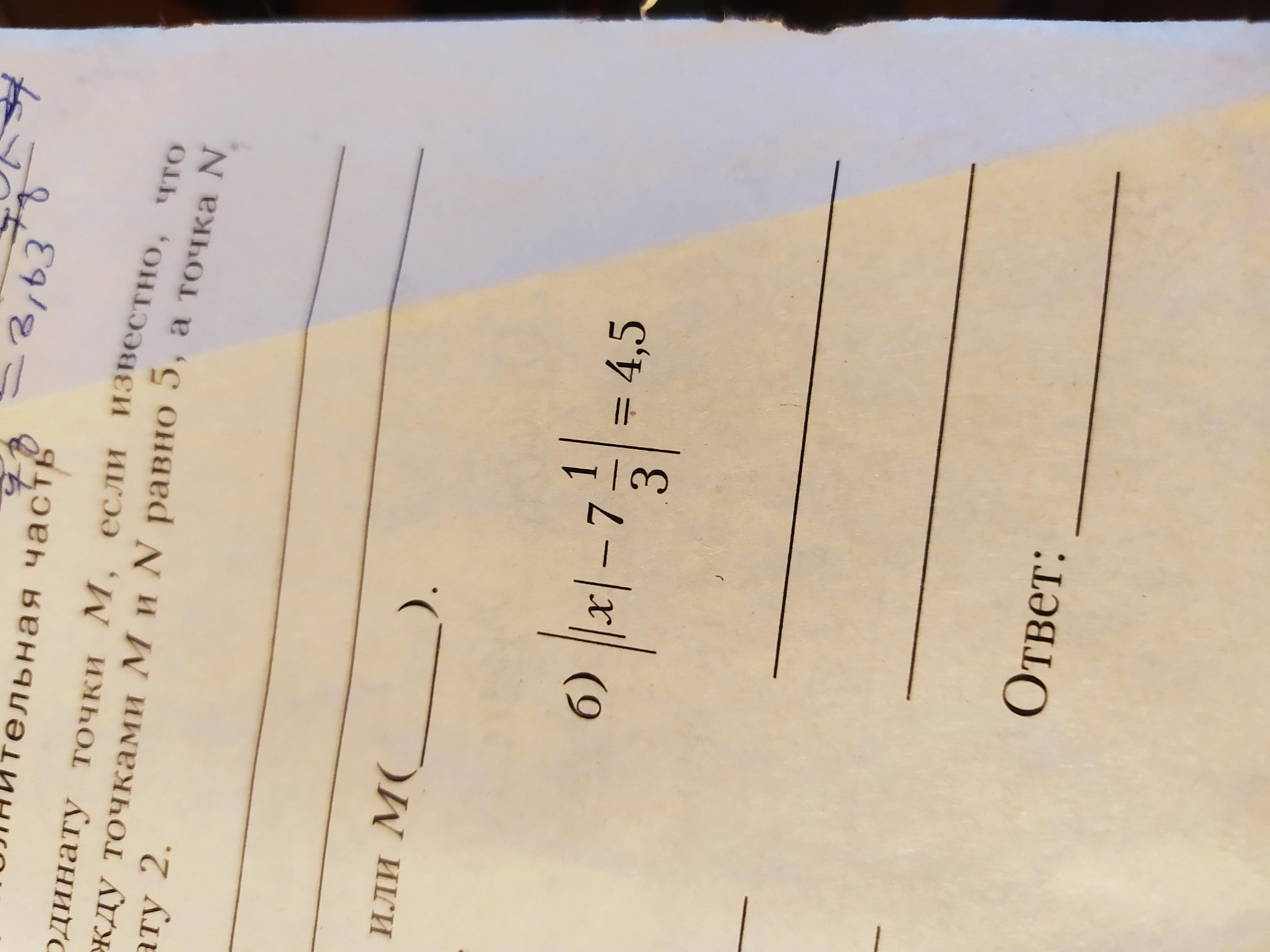
Ответы
Автор ответа:
2
Пошаговое объяснение:
Число под модулем может быть как положительное , так и отрицательное
Значит , при раскрытии первого модуля мы получим систему уравнений :
Поскольку х у нас по модулю , значит его значение может быть как отрицательным так и положительным , по этому у нас получится четыре корня этого уравнения :
Похожие вопросы
Предмет: Математика,
автор: ptzмаксим
Предмет: Математика,
автор: Hellobaby11
Предмет: Литература,
автор: CrazyLemon2003
Предмет: Математика,
автор: Føxŷ12
Предмет: История,
автор: Данил22223