Предмет: Геометрия,
автор: Danilka228213
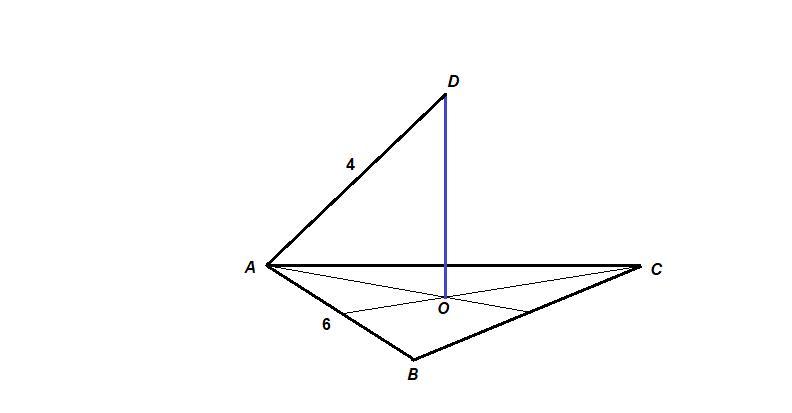
Через центр О правильного треугольника АВС проведена прямая ДО, перпендикулярная плоскости АВС. Найдите отрезок ДО, если АВ=6см, ДА=4см. Cрочно помогите, да.т 35 балов
Ответы
Автор ответа:
2
Ответ:
2 см
Объяснение:
АО - радиус окружности, описанной около правильного треугольника АВС.
,
где а - сторона треугольника.
см
Из прямоугольного треугольника AOD по теореме Пифагора:
см
Приложения:
Похожие вопросы
Предмет: Биология,
автор: ILLARION23
Предмет: Геометрия,
автор: Rbhbkkxvz361
Предмет: Математика,
автор: smertinat
Предмет: Русский язык,
автор: valeron0510