Предмет: Математика,
автор: grypepe
срочно
помогите найти первообразную!!!!!!!!
Приложения:
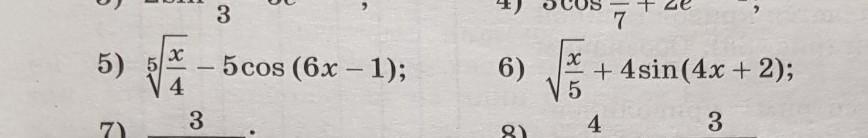
Ответы
Автор ответа:
1
Пошаговое объяснение:
Используем следующие формулы:
5) Преобразуем выражение и найдем первообразную:
6) Преобразуем выражение и найдем первообразную:
Похожие вопросы
Предмет: Алгебра,
автор: rimlininchik
Предмет: Русский язык,
автор: Djemmely
Предмет: Математика,
автор: yulak101
Предмет: Русский язык,
автор: Helping3r5
Предмет: Химия,
автор: Yarovayana