Предмет: Математика,
автор: Akosyamin1
Можете решить 18задание
Докажите что заданные числовые последовательности {Xn} n=1,2,3 определены при всех достаточно больших значениях номеров n, и вычислите их пределы.
Приложения:
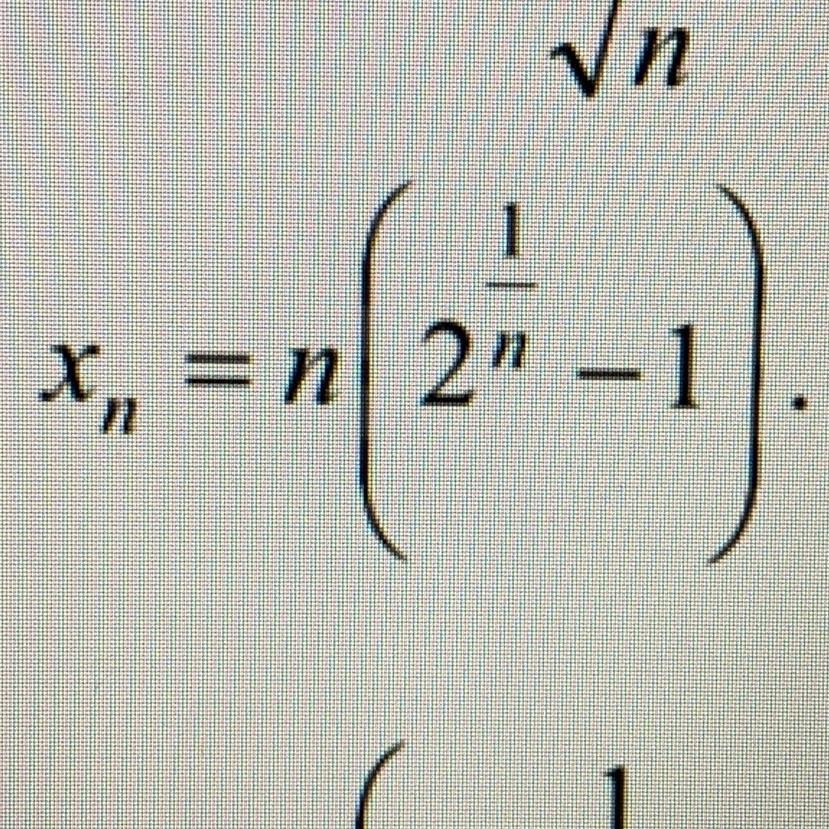
Ответы
Автор ответа:
1
Ответ: lim xn=ln2.
Пошаговое объяснение:
Так как n≠0, то выражение 2^(1/n), а вместе с ним и выражение xn=n*[2^(1/n)-1], определены при любом натуральном n. Для нахождения предела последовательности положим 1/n=m. Тогда n=1/m, при n⇒∞ m⇒0 и выражение примет вид: (2^m-1)/m. Если m⇒0, то 2^m-1⇒0 и мы имеем неопределённость вида 0/0. Для нахождения её предела используем правило Лопиталя: (2^x-1)'=(2^x)*ln2, x'=1, поэтому искомый предел равен пределу выражения (2^x-1)'/x'=(2^x)*ln2 при x⇒0. Очевидно что этот предел равен ln2.
Похожие вопросы
Предмет: Биология,
автор: nrassadina55
Предмет: Физика,
автор: skymaks
Предмет: Математика,
автор: Pigma47
Предмет: Русский язык,
автор: 210980polina
Предмет: Физика,
автор: 0624700