Предмет: Математика,
автор: likanerskaya
Найти производную
Помогите пж
Приложения:
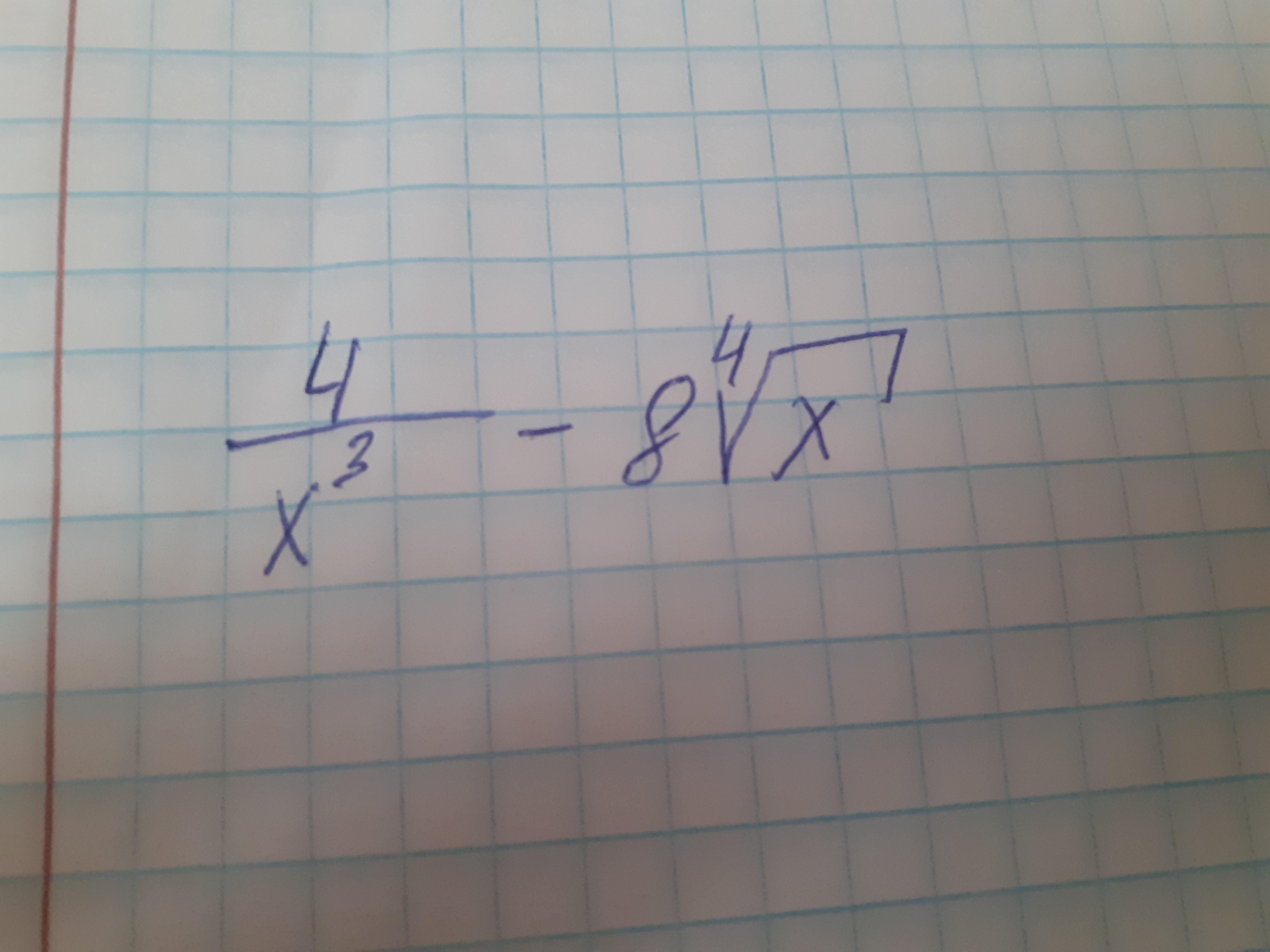
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Преобразуем данное выражение:
Используем следующие формулы:
Вычислим производную:
Похожие вопросы
Предмет: Русский язык,
автор: Alxazovakemale
Предмет: Алгебра,
автор: 123FM
Предмет: Русский язык,
автор: bekhruz2105
Предмет: Окружающий мир,
автор: OlgaPrytkova
Предмет: Математика,
автор: gugugaga234