Question

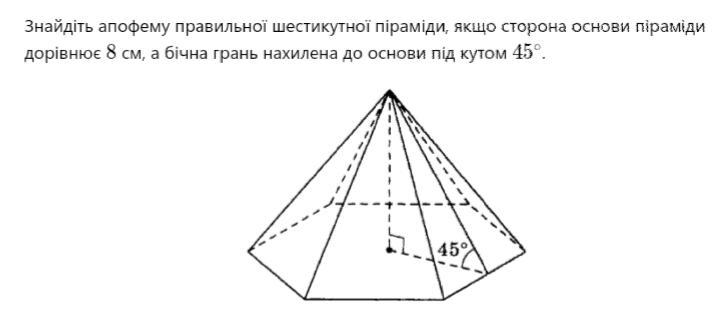
Геометрия, 11 класс
Срочно!

Answer 1

Ответ:

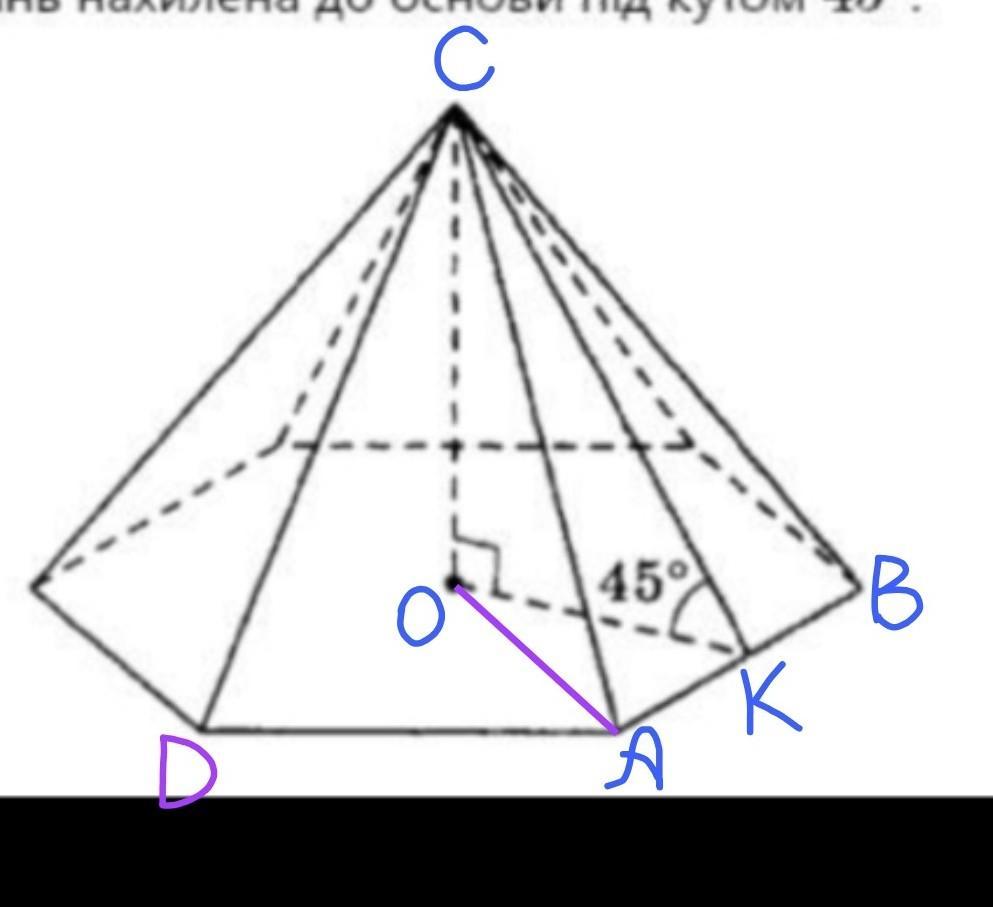
Обозначим некоторые вершины углов пирамиды как обозначено на рисунке.

• СО – высота, проведенная из вершины пирамиды к основанию. Точка О так же будет являться центров основания пирамиды, так как пирамида правильная

СК и ОК – перпендикуляры, лежащие на боковой грани АСВ и основании пирамиды соответственно.

Так как данная пирамида правильная, а точка С – вершина этой пирамиды, то СК так же будет являться апоферой и высотой боковой грани.

• Угол между плоскостями – это угол между перпендикулярами, лежащих на этих плоскостях, проведенных к одной точке на линии пересечения плоскостей.

То есть если угол между боковой гранью и основанием пирамиды равен 45°, то угол СКО=45° так же.

• Рассмотрим ∆АСВ.

Так как пирамида правильная, то её боковые грани равны, то есть СА=СВ, значит ∆АСВ – равнобедренный с основанием АВ.

Высота равнобедренного треугольника, проведенная к основанию так же является медианой.

Тогда СК – медиана, а АК=КВ.

Так как из условия АВ=8 см, то АК=4 см.

• Рассмотрим основание пирамиды.

Проведем ОА. Отрезок, проведённый из центра правильного многоугольника к вершине его угла будет являться биссектрисой этого угла.

Следовательно ОА – биссектриса угла DAB.

Каждый угол правильного шестиугольника равен 120°.

Следовательно угол ОАВ=угол DAB÷2=120°÷2=60°.

• Рассмотрим ∆ОАК.

Так как ОК – перпендикуляр, то ∆ОАК – прямоугольный с прямым углом ОКА.

В прямоугольном треугольнике:

tg(угол ОАК)=AK/OK

tg(60°)=4/OK

$\sqrt{3} = \frac{4}{OK} \\ OK = \frac{4 \sqrt{3} }{3}$

• Рассмотрим ∆СОК

Так как СО – высота пирамиды, то ∆СОК – прямоугольный с прямым углом СОК.

В прямоугольном треугольнике сумма острых углов равна 90°. Следовательно:

Угол ОСК=90°–угол СКО=90°–45°=45°

Получим угол ОСК=угол СКО, тогда ∆СОК – равнобедренный с основанием СК. Значит

$CO=KO = \frac{4 \sqrt{3} }{3}$

По теореме Пифагора в ∆СОК

СК²=КО²+СО²

$CK {}^{2} = ( \frac{4 \sqrt{3} }{3} ) {}^{2} + {( \frac{4 \sqrt{3} }{3} )}^{2} \\ CK {}^{2} = \frac{2 \times 16 \times 3}{9} \\ CK {}^{2} = \frac{32}{3} \\ CK = \sqrt{ \frac{32}{3} }$

$Otvet: \: \sqrt{ \frac{32}{3} }$