Question

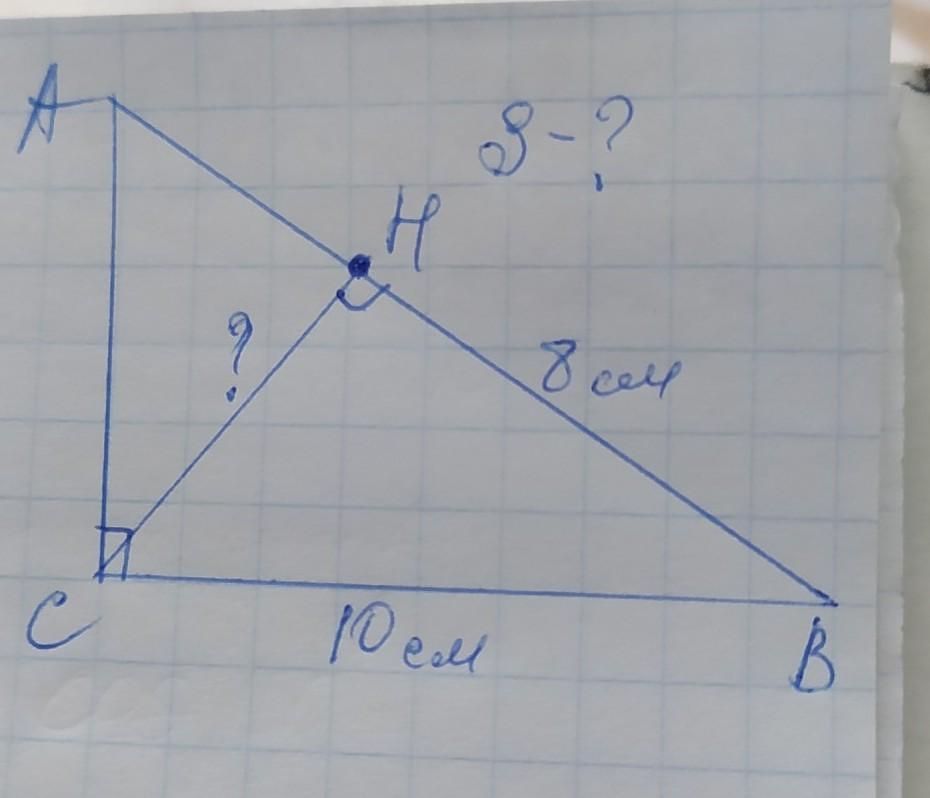
В прямоугольном треугольнике АВС с прямым углом С проведена высота СН из прямого угла. Катет ВС=10 см, а его проекция на гипотенузу – 8 см. Найти высоту треугольника АВС и его площадь.

Answer 1

Ответ:

СН=6см

S=37,5см²

Объяснение:

найдём высоту СН по теореме Пифагора:

СН²=ВС²–ВН²=10²–8²=100–64=36

СН=√36=6см

Высота в прямоугольном треугольнике, проведённая из вершины прямого угла делит его на 2 прямоугольных треугольника подобных данному, а также эти 2 полученных треугольника подобны между собой, поэтому ∆АСН~∆ВСН

$\\ \frac{bc}{ac} = \frac{bh}{ch}$

$\\ \frac{10}{ac} = \frac{8}{6}$

перемножим числитель и знаменатель этих дробей между собой крест накрест:

8×АС=10×6

8АС=60

АС=60÷8

АС=7,5

Площадь прямоугольного треугольника вычисляется по формуле:

$\\ s = \frac{1}{2} \times ac \times bc = \frac{1}{2} \times 7.5 \times 10 = \\ = \frac{75}{2} = 37.5$