Предмет: Алгебра,
автор: Почемучка91
Алгебра, 8 класс
Пользуясь соотношением между средним арифметическим и средним геометрическим двух положительных чисел, докажите неравенство: №970(б)
Подробно, пожалуйста :(
Приложения:
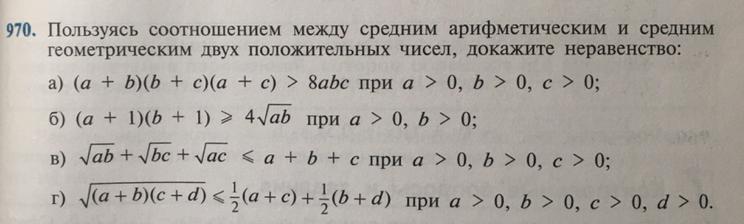
mawos:
что это за учебник
Макарычев, просвещение 2018, углубленный уровень
Только из ГД3 не надо, пожалуйста)
Ответы
Автор ответа:
1
- выражение всегда неотрицательно,
- выражение всегда неположительно.
Неравенство доказано.
Спасибо большое
Похожие вопросы
Предмет: Алгебра,
автор: АнстасияКотова
Предмет: Математика,
автор: pro10027
Предмет: Математика,
автор: pro10027
Предмет: Химия,
автор: 3456725
Предмет: Математика,
автор: danielyan927p4eacd