Question

У трапеції Abcd бічні сторони AB і CD перетинаються в точці H, AB:BH=2:3. BC менша основа. Знайдіть основи трапеції, якщо їх різниця дорівнює 12​

Answer 1

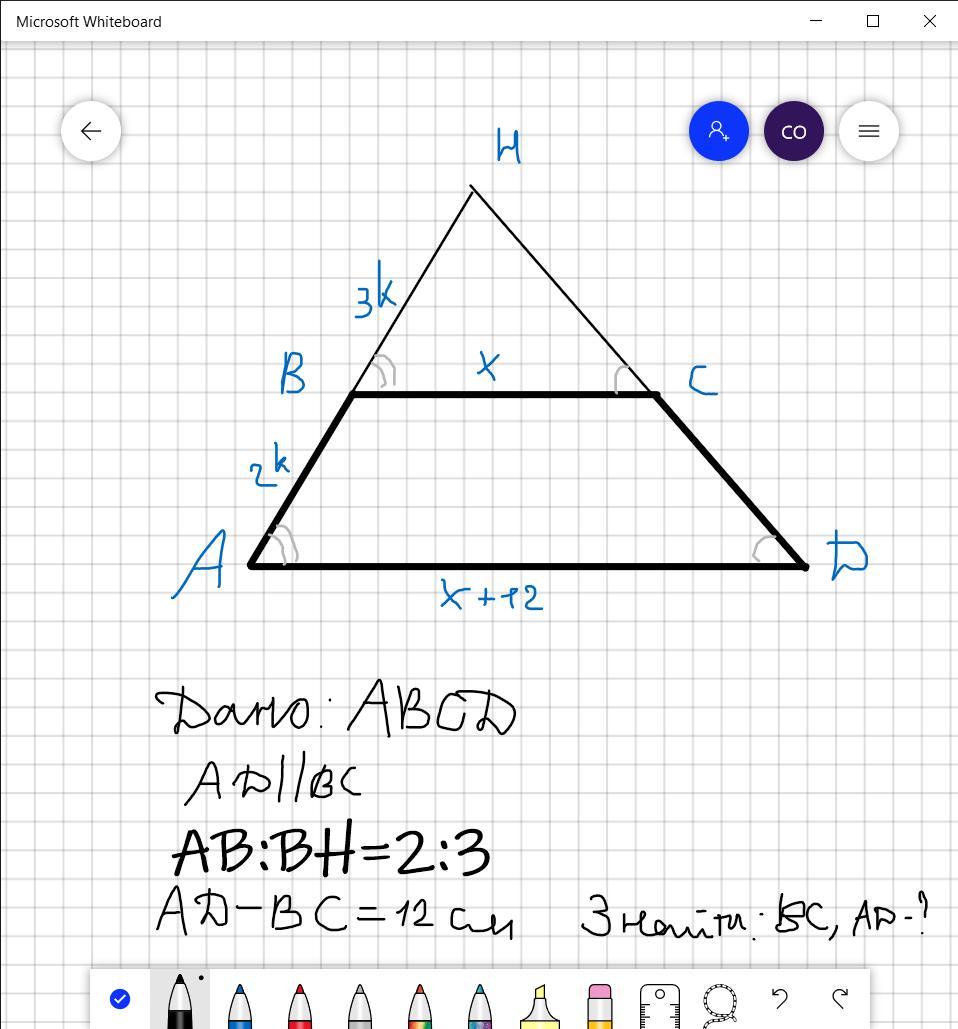
На фото малюнок і дано

Розв'язання. Оскільки основи трапеції паралельні, то CD--січна для ВС і АD =>

∠HDA=∠HCB як відповідні кути,

АВ також січна, тож ∠НАD=∠НВС як відповідні

Кут ∠Н--спільний для трикутників ΔНВС і ΔHAD.

Отже, ΔНВС і ΔHAD подібні за трьома кутами.

Позначимо ВН=3k, AB=2k. Тоді АН=АВ+ВН=2k+3k=5k

АН:ВН=АD:ВС

Позначимо ВС=х, АD=х+12

Тоді 5k:3k=(х+12):х

5:3=(х+12):х

маємо пропорцію

5х=3(х+12)

5х=3х+36

5х-3х=36

2х=36 | : 2

x=18 см

Отже, ВС=х=18 см

АD=х+12=18+12=30 см

Відповідь: 18 см; 30 см