Предмет: Математика,
автор: Kazakhstan222
970 решите системы неравенств.
Приложения:
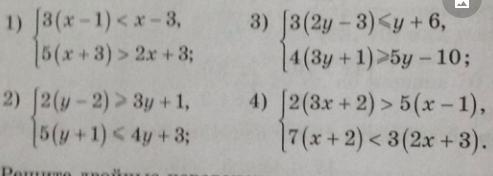
Ответы
Автор ответа:
7
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: levapv8
Предмет: Алгебра,
автор: venera055
Предмет: Алгебра,
автор: alk456
Предмет: Математика,
автор: nehanastasya