Предмет: Алгебра,
автор: mustafinleon
Помогите пожалуйста с алгеброй. И пожалуйста, расскажите как вы пришли к такому выводу, с объяснением и решением.
Приложения:
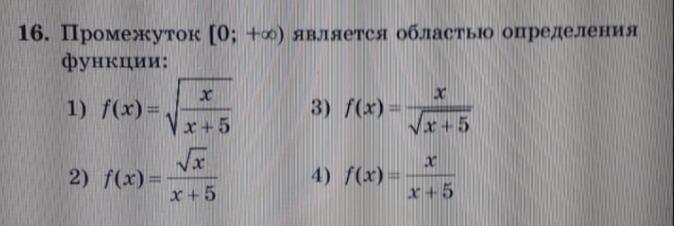
Ответы
Автор ответа:
1
определим у данный функций области определения
1)
ОДЗ: (-∞;-5)∪[0;+∞)
2)
ОДЗ: [0;+∞)
3)
ОДЗ: (-5;+∞)
4)
ОДЗ: (-∞;-5)∪(-5;+∞)
Значит ответ под 2)
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Химия,
автор: SWAGFOX16
Предмет: Алгебра,
автор: kostichevs
Предмет: Обществознание,
автор: matinurieva
Предмет: Информатика,
автор: Bekbek0101