Question

- Докажите, что если биссектриса внешнего угла треугольника параллельна стороне треугольника, то треугольник равнобедренный.​

Answer 1

Доказательство: (рисунок в помощь)
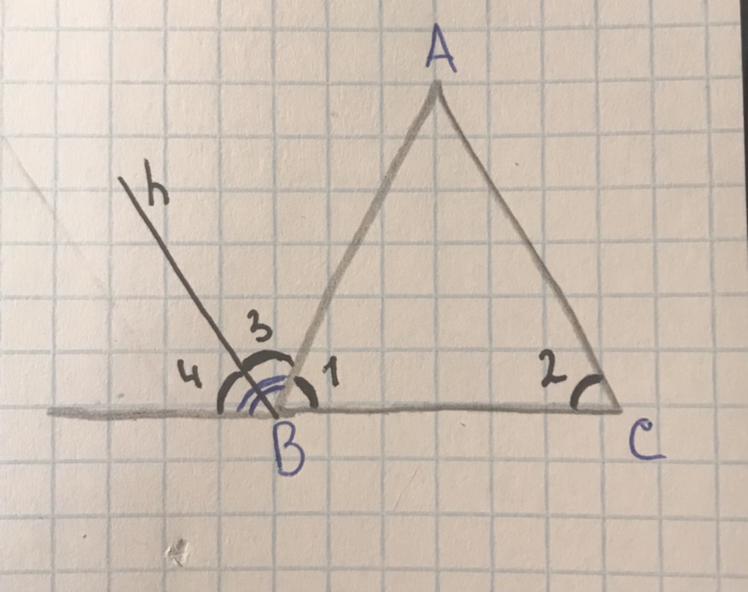
Биссектриса h внешнего угла B делит этот угол напополам. То есть одна половина внешнего угла равна внутреннему углу 1. А т.к. биссектриса h параллельна стороне AC, то из параллельности прямых следует, что соответственные углы равны, т.е. углы 2 и 3 равные. А так как половина внешнего угла (угол 3) равна внутреннему углу 1, то угол 1= углу 2. А эти углы- углы при основании ВС, если углы при основании равны- треугольник равнобедренный, что и требовалось доказать.
Надеюсь, понятно объяснила)