Предмет: Математика,
автор: Tam3rlaN
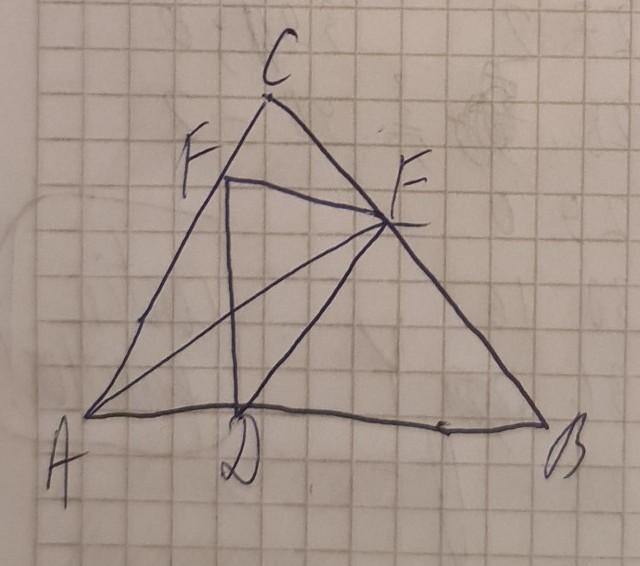
площадь треугольника ABC равна 10 см². также известно что AD= 2см, DB= 3см. если площадь треугольника ABE равна площади четырехугольника DBEF найдите площадь треугольника ABE
Приложения:
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
из рисунка видно,(правда коряво смотрится), но все же, четырех угольник ДБЕФ- трапеция, а отрезки(стороны) АС и DЕ, АВ и ЕF. взаимно параллельны ⇒ AD=EF=2, AF=DE,
из ΔАВС найдем высоту, опущенную на сторону АВ=5,
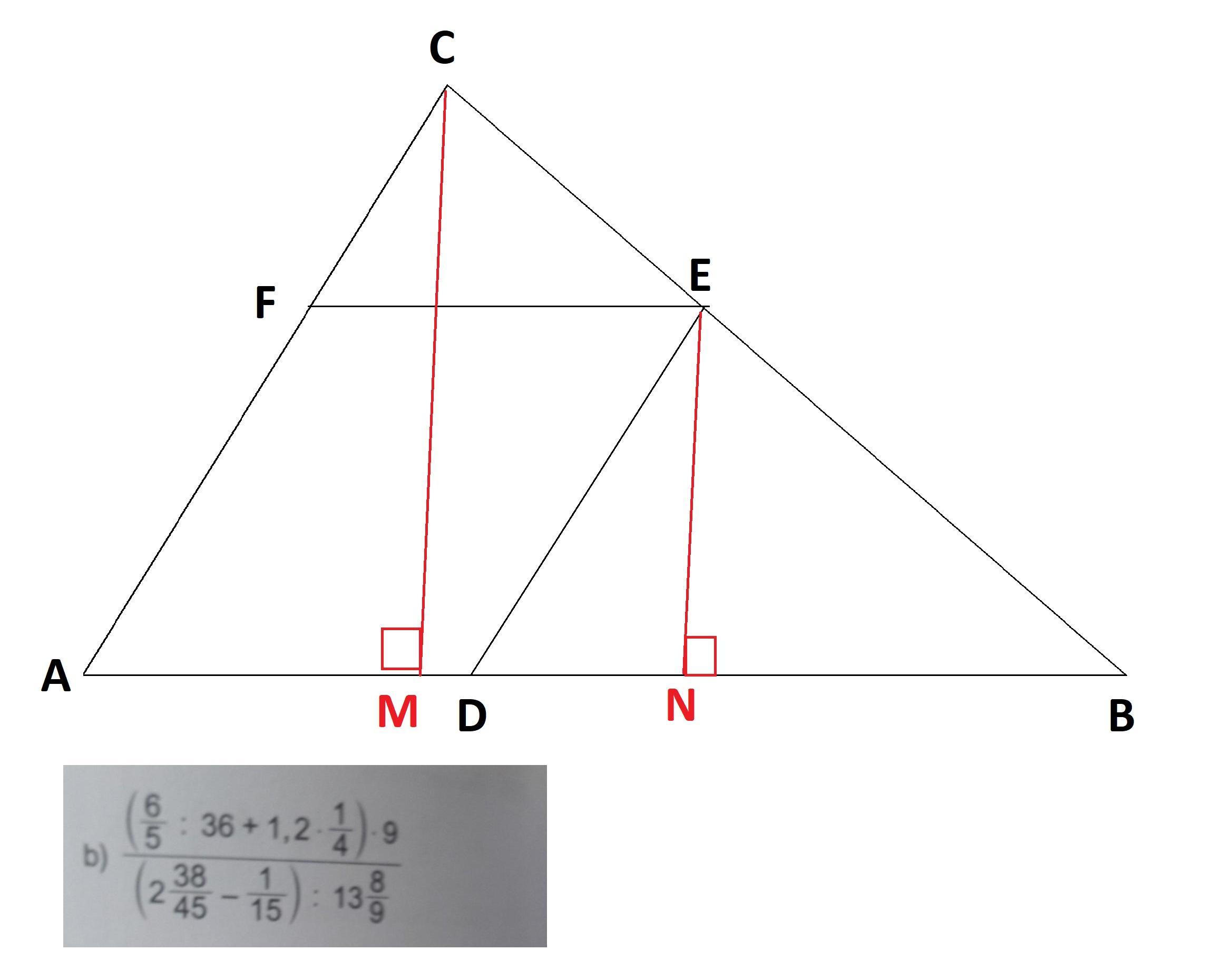
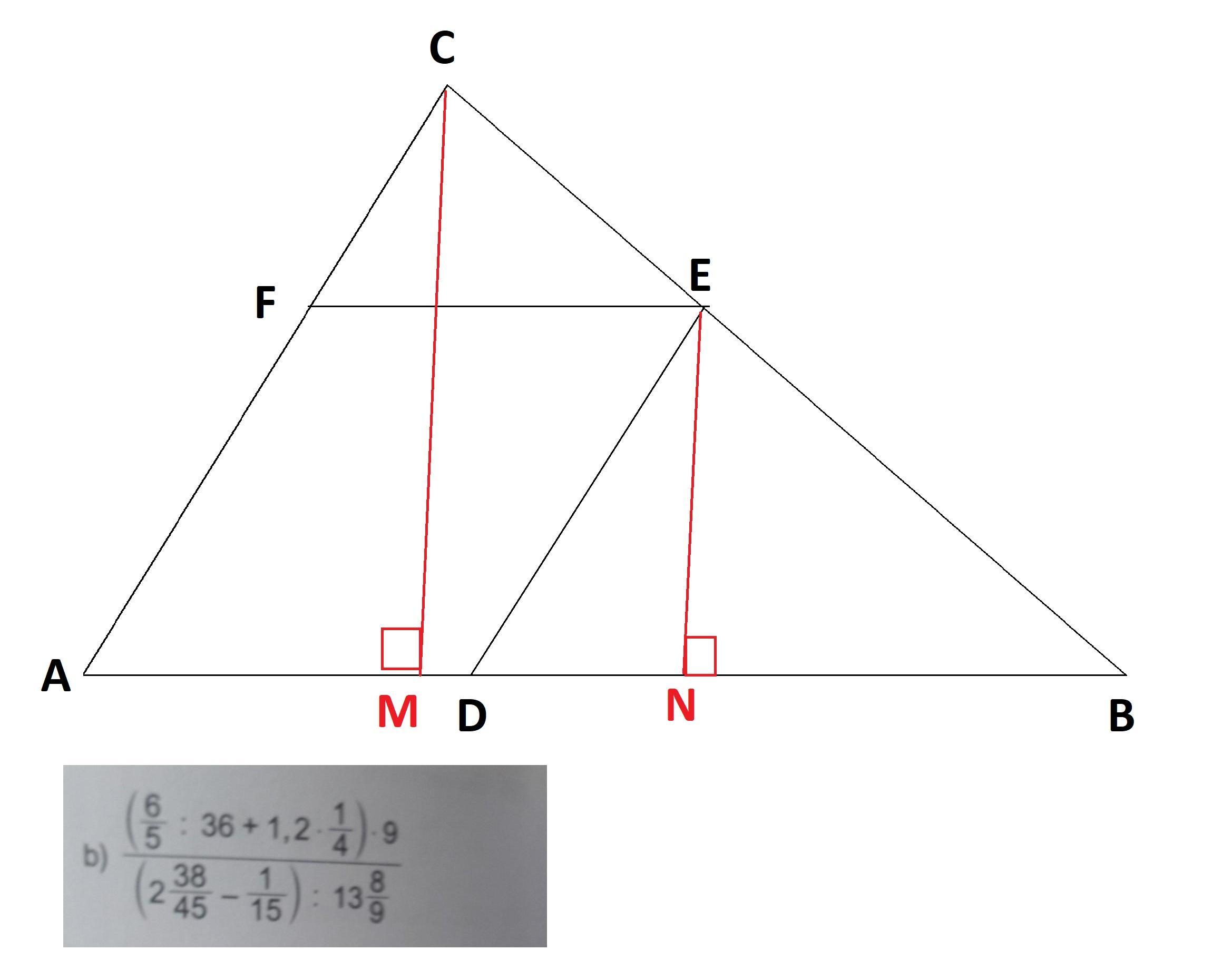
рассмотрим подобие ΔАCВ и ΔDEB,
проведем высоты CM и EN, подобие сохранится. ⇒
S= 0.5* EN*DB=0.5*2.4*3=3.6
Приложения:
Tam3rlaN:
ответ должен быть целым числом. варианты ответа: а)4 б)5 с)6 д)7 е)8
там отрезки не паралельны
Похожие вопросы
Предмет: Математика,
автор: Rakhmanovatanya
Предмет: Литература,
автор: atarmerz
Предмет: Математика,
автор: lazukin1745
Предмет: Математика,
автор: ммм356
Предмет: Алгебра,
автор: Ангелина22325