Предмет: Математика,
автор: badoj47614
Помогите с задачами. развернуто пожалуйста!)
Приложения:
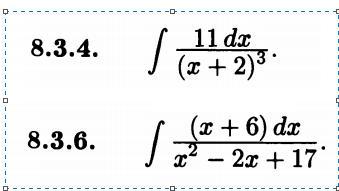
Ответы
Автор ответа:
3
Ответ:
834
836
делаем в числителе производную знаменателя:
(x^2-2x+17)' = 2x-2
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Английский язык,
автор: leonid32
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: Ян231