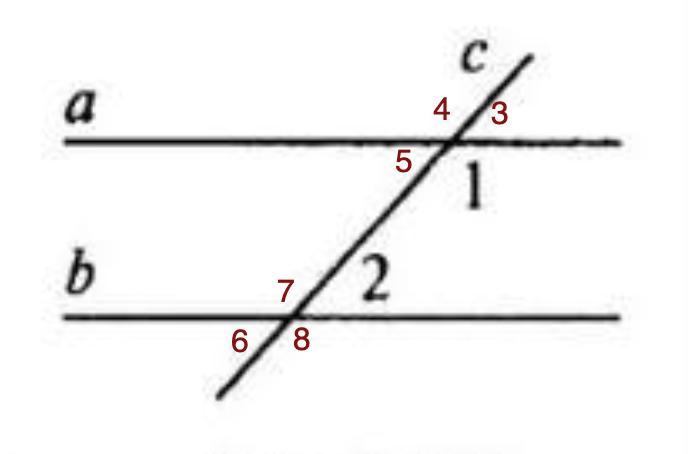
1.Дано: а||b, с — секущая, ∠1 — ∠2 = 102° (рис. 3.173). Найти: Все образовавшиеся углы.
2.Дано: ∠1 = ∠2, ∠3 = 140° (рис. 3.174). Найти: ∠4.
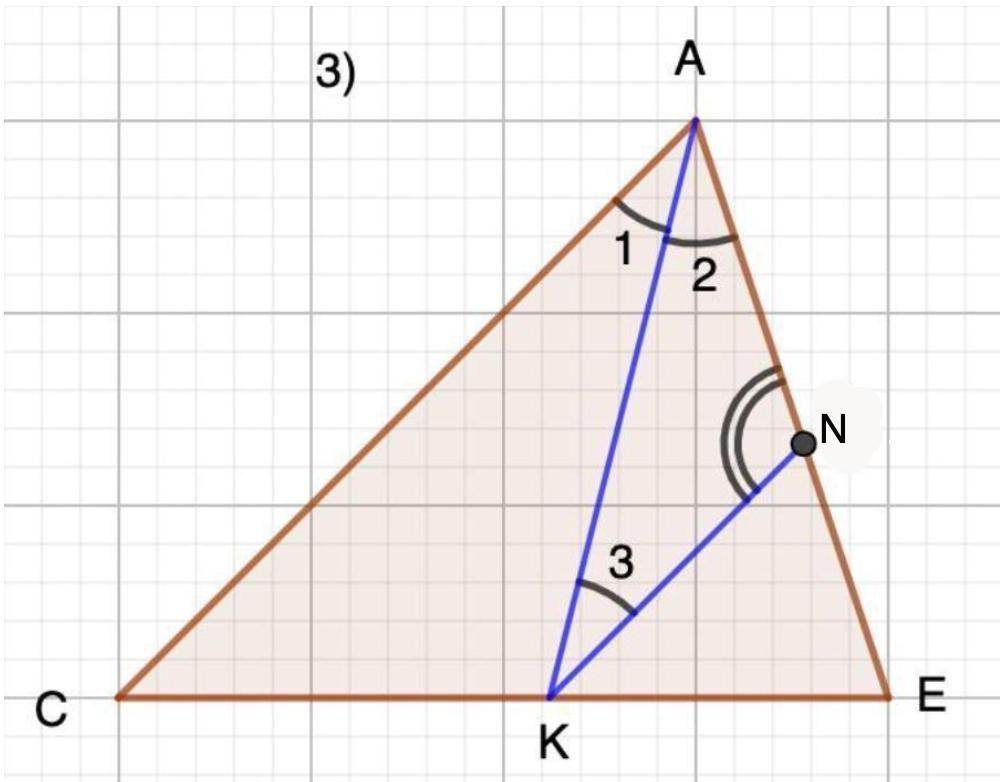
3.Отрезок АК — биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если ∠CAE = 78°.
Помогите пожалуйста. Срочно (№4 не надо)!

Ответы
Объяснение:
1. Дано: a║b, c - секущая;
∠1-∠2=102°
Найти: все образовавшиеся углы.
Решение:
1) ∠1-∠2=102° ⇒ ∠1=102°+∠2
2) ∠1+∠2=180° - внутренние односторонние при a║b и секущей с.
или (102°+∠2)+∠2=180°
2·∠2=78° ⇒∠2=39°
∠1=102°+∠2=102°+39°=141°
3) ∠1=∠4=141° - вертикальные;
∠3=180°-∠1=180°-141°=39° - смежные;
∠5=∠3=39° - вертикальные;
4) ∠6=∠2=39° - вертикальные;
∠7=180°-∠2=180°-39°=141° - смежные;
∠8=∠7=141° - вертикальные.
2. Дано: ∠1=∠2; ∠3=140°.
Найти: ∠4.
Решение:
1) ∠1=∠2 - соответственные при прямых a и b и секущей АВ.
⇒a║b.
2) ∠3+∠4=180° - внутренние односторонние при a║b и секущей ВС.
140°+∠4=180° ⇒ ∠4=180°-140°=40°.
3. Дано: ΔСАЕ; АК - биссектриса;
КN║СА ; ∠САЕ=78°
Найти: углы ΔAKN.
Решение:
1) ∠1=∠2=78°:2=39° (АК - биссектриса);
∠1=∠3 =39° (накрест лежащие при KN║AC и секущей АК);
⇒ ∠2=∠3=39°
2) Рассмотрим ΔAKN.
∠2=∠3=39° (п.1)
⇒∠ANK=180°-(∠2+∠3)=180°-(39°+39°)=102° (сумма углов треугольника)