Предмет: Математика,
автор: rinatvit82
Найти предел функции.
Приложения:
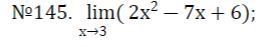
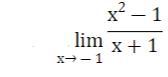

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
в третьем пределе поделим все члены числителя и знаменателя на наивысшую степерь знаменателя
Похожие вопросы
Предмет: Физика,
автор: ник66любитель
Предмет: Математика,
автор: nasibullinaalb2
Предмет: Английский язык,
автор: kristinasmirno5
Предмет: Математика,
автор: gels5344Inetka
Предмет: Математика,
автор: ay7alv