Предмет: Геометрия,
автор: alyonablox
ПОМОГИТЕ СРОЧНО
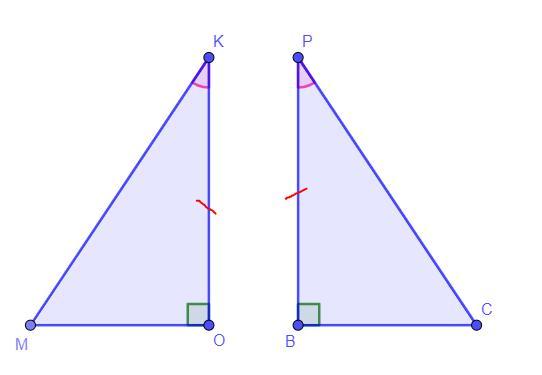
В треугольниках ОКМ и BPC углы О и В равны 90о , КО=ВР, угол К равен углу Р. Укажите признак равенства этих треугольников:
Укажите правильный вариант ответа:
по гипотенузе и катету
по гипотенузе и острому углу
по двум катетам
по катету и острому углу
Ответы
Автор ответа:
4
Ответ:
По катету и острому углу
Объяснение:
Дано: ∠O = ∠B = 90°, ∠K = ∠P, KO = BP
Доказать: ΔKOM = ΔBPC
Доказательство: Треугольник ΔKOM = ΔBPC по второму признаку равенства треугольников, так как по условию ∠O = ∠B = 90°, ∠K = ∠P, KO = BP, то есть треугольник ΔKOM = ΔBPC по острому и углу и катету, так как по условию треугольник ΔKOM и ΔBPC - прямоугольные
(∠O = ∠B = 90°), острые углы равны (∠K = ∠P) и равны катеты
(KO = BP).
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аня1103
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: Танюшка11111111
Предмет: Математика,
автор: lolkeklolkek123
Предмет: Русский язык,
автор: mixailova1985