Предмет: Математика,
автор: svetahit
СРООООООООООООООЧННООООО"!!!!!!!!!!!!!!!!!!!!!!!!
Медиана bm треугольника abc является диаметром окружности, пересекающей сторону bc в ее середине. Длина стороны ac равна 4. найдите радиус описанной окружности треугольника ABC
Ответы
Автор ответа:
0
По известному утверждению если диаметр является стороной определенного треугольник то он прямоугольный , воспользуемся этим .
Если
по свойству касательной и секущей имеем такое соотношение

тогда , проведем LM, треугольник
, проведем LM, треугольник  , тогда
, тогда
 , отудого
, отудого

Найдем угол , по теореме косинусов
, по теореме косинусов

сторона
тогда радиус по теореме синусов равен

Ответ 2
Если
по свойству касательной и секущей имеем такое соотношение
тогда
Найдем угол
сторона
тогда радиус по теореме синусов равен
Ответ 2
Приложения:
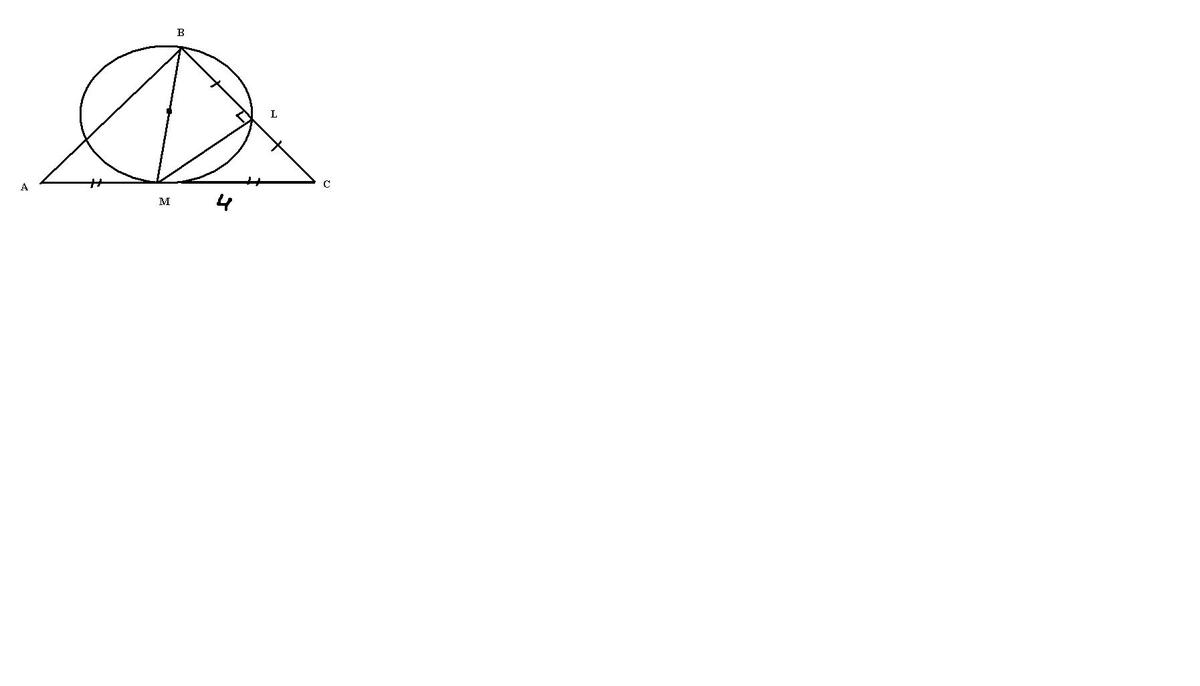
Похожие вопросы
Предмет: Математика,
автор: prokras0909
Предмет: Химия,
автор: anastasiaprozorova20
Предмет: Қазақ тiлi,
автор: kasymovaanel0
Предмет: Математика,
автор: Liliya1308