Предмет: Алгебра,
автор: d8052000
Помогите эти две номера решить срочно до субботы.
Приложения:
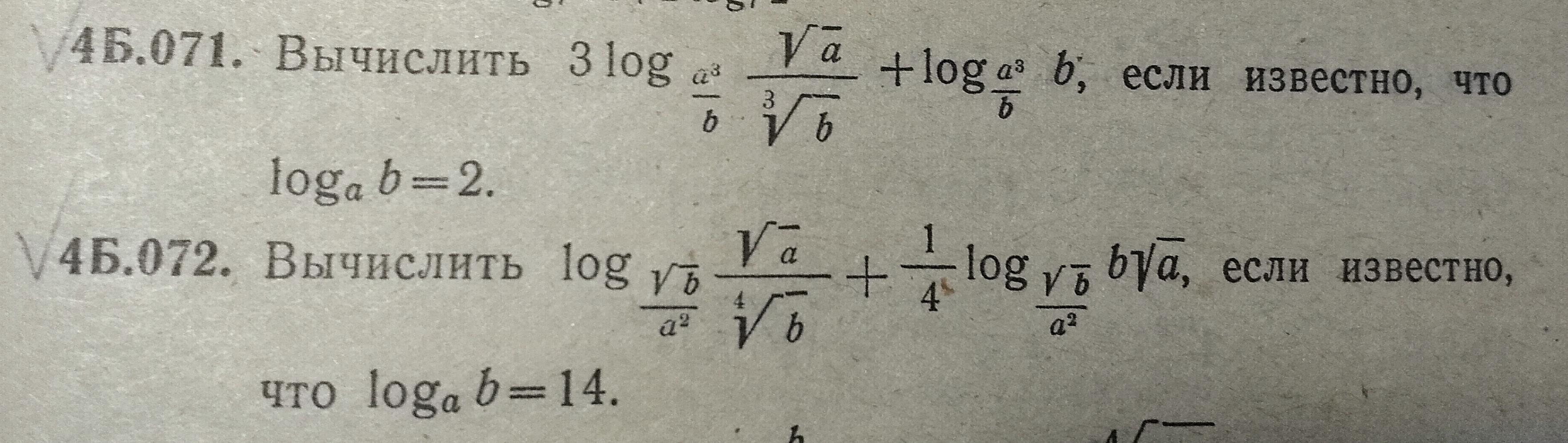
Ответы
Автор ответа:
1
d8052000:
Во втором номере верно, а в первом разве не получится 1/3?
У меня конце учебнике там ответы: 4Б.071 (Ответ: 3/2), а в 4Б.072 (Ответ: 1/8). В 4Б.072 верное, а вы можете проверить на всякий случай что-бы получилось точный ответ, только на ваш 1 ответ я сомневаюсь.
решение исправила
Отлично, спасибо за помощь.
Похожие вопросы
Предмет: Биология,
автор: Katysha4255
Предмет: Русский язык,
автор: iosich12
Предмет: Другие предметы,
автор: Трансаэро7625
Предмет: История,
автор: ghghgh2345
Предмет: Информатика,
автор: никитикитук