Предмет: Алгебра,
автор: nuykonka19971
При каких натуральных значениях уравнения имеют более/менее одного корня?
Приложения:

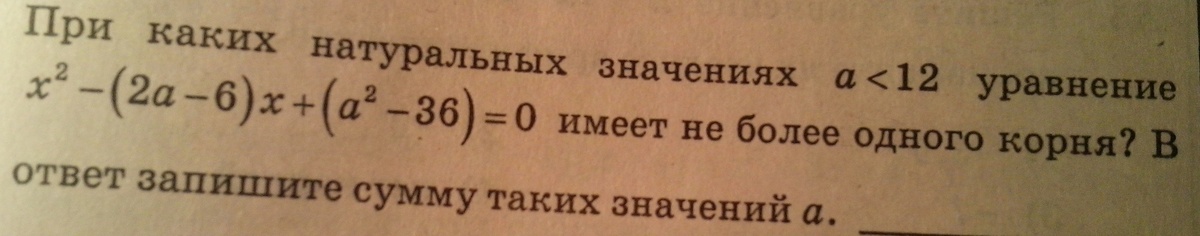


Ответы
Автор ответа:
0
1) Уравнение x²-(2a-4)x+(a²-25) имеет 1 корень при D = 0.
D = b²-4ac
D = (-(2a-4))²-4*1*(a²-25) = 4a²-16a+16-4a²+100
-16a+116 = 0
a = 116/16 = 29/4.
Чтобы было 2 корня, D должно быть больше 0,
т.е. а<29/4, таких значений бесконечное множество.
2) Уравнение x²-(2a-6)x+(a²-36) имеет не более 1, т.е.1 корень при D = 0, а менее , т.е. ни одного при D < 0.
D = b²-4ac
D = (-(2a-6))²-4*1*(a²-36) = 4a²-24a+36-4a²+144
-24a+180 = 0
a = 180/24 =15/2 - один корень,
при a >15/2 - ни одного корня.
D = b²-4ac
D = (-(2a-4))²-4*1*(a²-25) = 4a²-16a+16-4a²+100
-16a+116 = 0
a = 116/16 = 29/4.
Чтобы было 2 корня, D должно быть больше 0,
т.е. а<29/4, таких значений бесконечное множество.
2) Уравнение x²-(2a-6)x+(a²-36) имеет не более 1, т.е.1 корень при D = 0, а менее , т.е. ни одного при D < 0.
D = b²-4ac
D = (-(2a-6))²-4*1*(a²-36) = 4a²-24a+36-4a²+144
-24a+180 = 0
a = 180/24 =15/2 - один корень,
при a >15/2 - ни одного корня.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: uarovauigulina
Предмет: Английский язык,
автор: sartov44
Предмет: Математика,
автор: lyubo4ka