Предмет: Алгебра,
автор: madam079
Помогите пожалуйста решить задание на дифференциал по алгебре
Приложения:
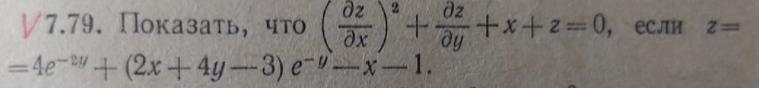
Ответы
Автор ответа:
2
теперь все сложим по действиям
что и требовалось доказать
Похожие вопросы
Предмет: Обществознание,
автор: lenslae1
Предмет: Математика,
автор: Dudh
Предмет: Алгебра,
автор: Kronox
Предмет: Обществознание,
автор: Lenaaaa111
Предмет: Английский язык,
автор: rtej