Предмет: Геометрия,
автор: kata67109
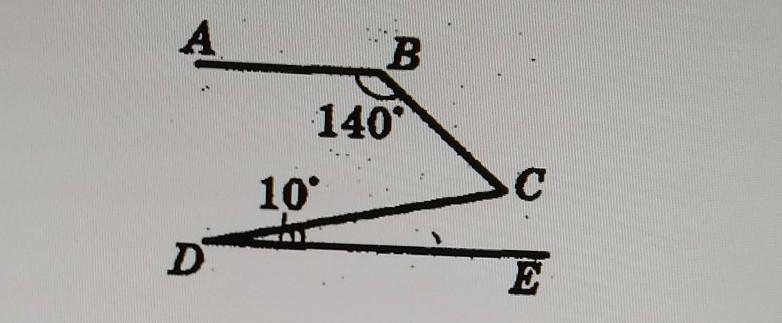
На рисунке АВ||DE. Найдите угол BCD, если ∠ABC = 140˚, ∠CDE = 10˚.
Приложения:
Ифигения:
50
а можно объяснение
Мне лень) это надо на бумажке писать...
блин. буду заранее благодарна если будет полный ответ
там нужно продолжить прямую ВС и работать с треугольником СДЕ, и все будет в ажуре.
угол СЕД будет равен 40, они с АВС односторонние
а внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
спасибо
Ответы
Автор ответа:
1
Объяснение:
Продлим BC до пересечения с DE
BC ⋂ DE = K
∠ BKD и ∠ABC - внутренние односторонние углы при AB||DE и секущей BC ⇒∠BKD = 180° - ∠ABC = 180° - 140° = 40°
∠BCD - внешний угол ΔDCK равен сумме двух внутренних углов Δ, не смежных с ним ⇒
∠BCD = ∠CDE + ∠CKD = 10° + 40° = 50°
Ответ: ∠BCD = 50°
Похожие вопросы
Предмет: Алгебра,
автор: mariyashevczov
Предмет: Химия,
автор: sana1986
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: 2255956
Предмет: Английский язык,
автор: nastz45678