Предмет: Алгебра,
автор: stemmaksk
Как решать эти примеры с логарифмом в степени? Помогите, пожалуйста.
(С решением и ответом)
Приложения:
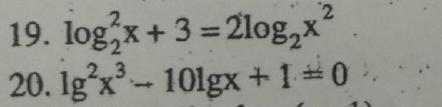
Ответы
Автор ответа:
1
Ответ:
Объяснение:
19) x>0, ( log2 x)^2 -4log2 x+3=0, y=log2 x, y^2-4y+3=0, y1=3, y2=1,
обратная замена: log2 x=3, x=2^3, x=8, log2 x=1, x=2, отв. 2; 8
20) x>0, (lgx^3)^2=(3*lgx)^2=9*(lgx)^2, тогда, 9*(lgx)^2-10lgx+1=0,
y=lgx, 9y^2-10y+1=0, D=100-36=64, y1=10+8 /18=1, y2=10-8 /18=1/9,
обратная замена: lgx=1, x=10, lgx=1/9, x=10^ 1/9 (^ -знак степени)
Автор ответа:
1
19
20
Похожие вопросы
Предмет: Алгебра,
автор: odnaklassnik
Предмет: Алгебра,
автор: ladykhilman
Предмет: Геометрия,
автор: AnnaNikky
Предмет: Математика,
автор: pchelka10