Предмет: Геометрия,
автор: milako97
Найдите острый угол между диагоналями прямоугольника со сторонами, равными 12 см и 8 см.
С рисунком.
Ответы
Автор ответа:
7
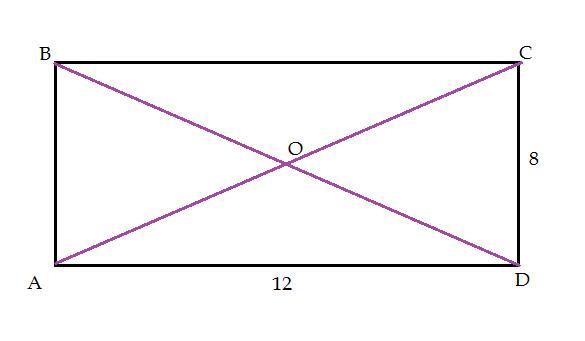
Дано: АВСD прямоугольник
AD=12. CD=8
найти <COD
решение:
в треугольнике ACD прямоугольном выразим AC по т. Пифагора
тогда OC=OD= 2√13
в треугольнике AOC по т. косинусов
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Novhal
Предмет: Английский язык,
автор: liloadamyan
Предмет: Английский язык,
автор: ruzlukasuka
Предмет: Математика,
автор: Катрин123456789014
Предмет: Химия,
автор: mana705335