Question

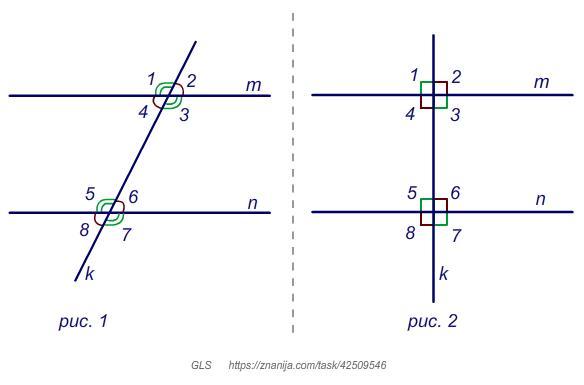
Параллельные прямые m и n пересечены секущей k. Выберите верные, соответствующие условию, утверждения:

1)Соответственные углы могут быть равны по 73°.
2)Внутренние накрест лежащие углы могут быть равны по 90°.
3)Сумма внутренних односторонних углов равна 180°.
4)Внутренние односторонние углы могут быть равны 127° и 63°.
5)Сумма соответственных углов может быть равна 180°.
6)Внутренние накрест лежащие углы могут составлять в сумме 90°.​

Answer 1

Ответ:

Верные ответы 1), 2), 3), 5), 6).

Объяснение:

Чтобы выбрать верные, соответствующие условию, утверждения, следует вспомнить, какие углы образуются, если две прямые пересечены секущей.

На рисунке параллельные прямые m и n пересечены секущей k.

Углы

• накрест лежащие: 4 и 6; 3 и 5;
• односторонние: 4 и 5; 3 и 6;
• соответственные: 1 и 5; 2 и 6 ; 3 и 7; 4 и 8.

Вспомним необходимые теоремы:

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

Рассмотрим утверждения задачи:

1) Соответственные углы могут быть равны по 73°. Верно.

Так как m║ n (k - cекущая), то соответственные углы равны и могут быть по 73°.

Например, могут быть ∠2 = 73° и ∠6 = 73°.

2) Внутренние накрест лежащие углы могут быть равны по 90°. Верно.

Так как m║ n (k - cекущая), то внутренние накрест лежащие углы равны и могут быть равны по 90°. Это возможно в случае, когда секущая k перпендикулярна параллельным прямым m и n (рис.2).

Например,  ∠4 = ∠6 = 90°.

3) Сумма внутренних односторонних углов равна 180°. Верно.

Согласно теореме 3, так как по условию m║ n (k - cекущая).

∠4 + ∠ 5 = 180°; ∠3 + ∠6 = 180°.

4) Внутренние односторонние углы могут быть равны 127° и 63°. Неверно.

Согласно теореме 3: если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

По условию m║ n (k - cекущая).

127° + 63° = 190° ≠ 180°.

5) Сумма соответственных углов может быть равна 180°. Верно.

Согласно теореме 2: если две параллельные прямые пересечены секущей, то соответственные углы равны.

Сумма соответственных углов  может быть равна 180° в случае, если каждый из них равен по 90°, то есть секущая перпендикулярна параллельным прямым (рис.2).

Например,  ∠1 = 90° и  ∠5 = 90°; ∠1 + ∠5 = 90° + 90° = 180°.

6) Внутренние накрест лежащие углы могут составлять в сумме 90°. Верно.

Согласно теореме 1: если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Тогда сумма накрест лежащих углов будет равна 90°, если их градусная мера равна по 45°.

Например,  ∠4 = 45° и  ∠6 = 45°; ∠4 + ∠6 = 45° + 45° = 90°.