Предмет: Алгебра,
автор: Saddno
Помогите пожалуйста решить неравенство с логарифмами
Приложения:
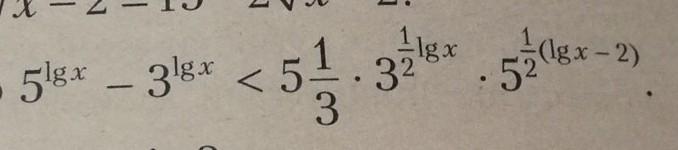
Simba2017:
не сразу
сначала все разделили на 15^(1/2*lgx)
а что потом
потом замена
там выйдет
(5/3)^(0.5lgx)-(3/5)^(0.5lgx) меньше 16/15
t-1/t меньше 16/15
все получилось, ответ такой-же как и у вас, спасибо
узнаете верный-напишите)))
хорошо
Ответы
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Литература,
автор: got4125
Предмет: История,
автор: мелена1
Предмет: Информатика,
автор: ВасяК
Предмет: Математика,
автор: foxaila
Предмет: Музыка,
автор: schoolboу