Question

Квадратичная функция, ее график и свойства. Урок 1

Выбери верные утверждения для функции y = 3(x – 9)2.

Верных ответов: 3

Область определения функции (–∞; +∞)

Вершина параболы – точка (–9; 0)

График функции проходит через точку (1; 192)

Промежуток возрастания x ∈ [9; +∞)

Множество значений функции (–∞; 0)

​

Answer 1

Ответ:

Верные утверждения:

1) ( - ∞; + ∞)- область определения данной функции;

2)график  функции проходит через точку (1; 192) ;

3) промежуток возрастания функции [ 9; +∞).

Объяснение:

Рассмотрим функцию

$y=3(x-9)^{2}$

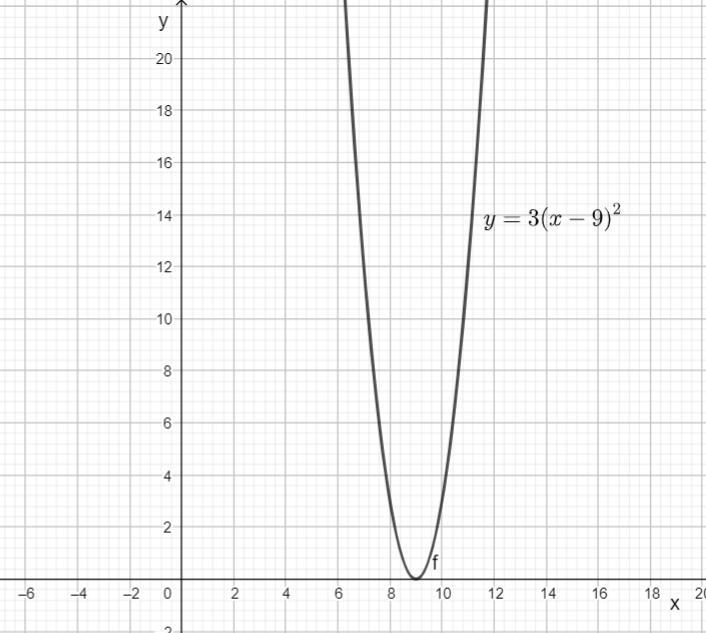
Графиком данной функции является парабола, ветви которой направлены вверх, с вершиной в точке (9; 0)

График данной функции во вложении.

Ответим на все все вопросы с помощью графика данной функции.

Область определения функции - это множество значений, принимаемых переменной х.

Значит, D(y) =( - ∞; + ∞)- область определения данной функции. Тогда это утверждение верно.

Вершина параболы в точке (9; 0). Значит, второе утверждение неверно.

Проверим проходит ли парабола через точку (1; 192). Для этого подставим координаты данной точки  и получим:

$192=3\cdot(1-9)^{2} ;\\192=3\cdot(-8)^{2} ;\\192= 3\cdot 64;\\192=192.$

Равенство верно, значит, график  функции проходит через точку

(1; 192) .

По рисунку определим, что функция возрастает на [ 9; +∞) и тогда это утверждение верно.

Множество значений функции - это множество значений, принимаемое переменной y.

E(y) = [ 0;+∞)- множество значений данной функции.

Поэтому последнее утверждение неверно.