Предмет: Алгебра,
автор: Sanya2306
Найти производные (если что, похідна=производная). Разбил на 4 части, чтоб за каждую дать по максимуму баллов. Это 4
Приложения:
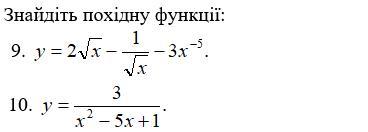
Ответы
Автор ответа:
1
Ответ:
9
10
Похожие вопросы
Предмет: Биология,
автор: kirialov98
Предмет: Биология,
автор: annnnna97
Предмет: Русский язык,
автор: cherepoc75
Предмет: Алгебра,
автор: 65кужз9
Предмет: Английский язык,
автор: Sovit