Предмет: Алгебра,
автор: evlaninkoviyia
решите пожалуйста , алгебра , 11 класс
Приложения:
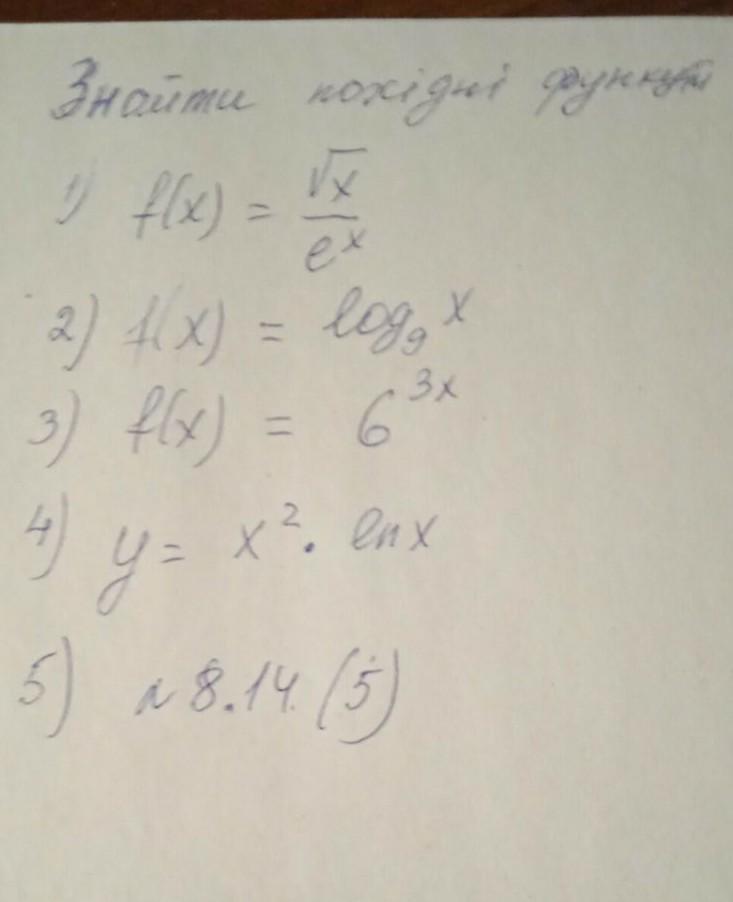
Ответы
Автор ответа:
1
Ответ:
1
2
3
4
Похожие вопросы
Предмет: Геометрия,
автор: vollec86
Предмет: Геометрия,
автор: leilaaristova
Предмет: Химия,
автор: 19zainka98
Предмет: Английский язык,
автор: Valeerkaaaaaa
Предмет: Українська мова,
автор: lizaborisovapop2cxfy