Предмет: Алгебра,
автор: tanya12097
Помогите пожалуйста прологарифмировать
Приложения:
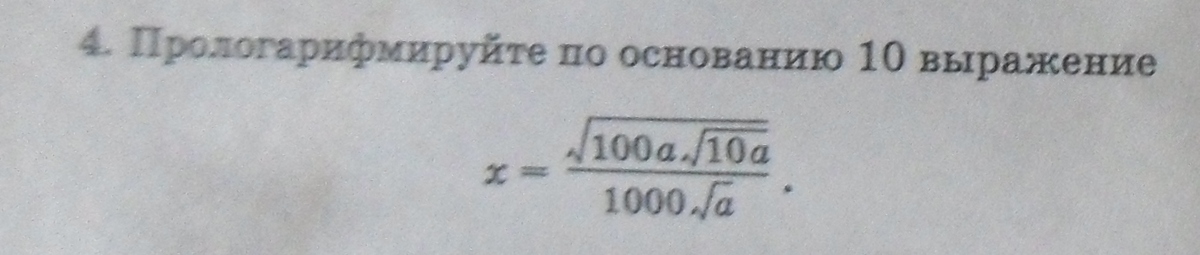
Ответы
Автор ответа:
0
Сначала преобразуем выражение, а потом прологарифмируем:
√(100а√(10а))/1000а = √(10^(5/2) × а^(3/2))/1000а = (10^(5/4) × а^(3/4))/1000а = 10^(5/4 - 3) × а^(3/4 - 1) = 10^(-7/4) × а^(-1/4).
Теперь логарифмируем:
lg(10^(-7/4) × a^(-1/4)) = lg(10^(-7/4)) + lg(a^(-1/4)) = -7/4 × lg10 + (-1/4) × lga = -(lga)/4 - 7/4.
√(100а√(10а))/1000а = √(10^(5/2) × а^(3/2))/1000а = (10^(5/4) × а^(3/4))/1000а = 10^(5/4 - 3) × а^(3/4 - 1) = 10^(-7/4) × а^(-1/4).
Теперь логарифмируем:
lg(10^(-7/4) × a^(-1/4)) = lg(10^(-7/4)) + lg(a^(-1/4)) = -7/4 × lg10 + (-1/4) × lga = -(lga)/4 - 7/4.
Автор ответа:
0
или ответ можно перевести в обычные дроби и записать так:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: akbdajana09
Предмет: Русский язык,
автор: plievas529
Предмет: Алгебра,
автор: AlenaCruz
Предмет: Математика,
автор: Аноним