Предмет: Алгебра,
автор: diana99444
637. Докажите тождество
Пожалуйста помогите
30-баллов!!!!!!
Приложения:
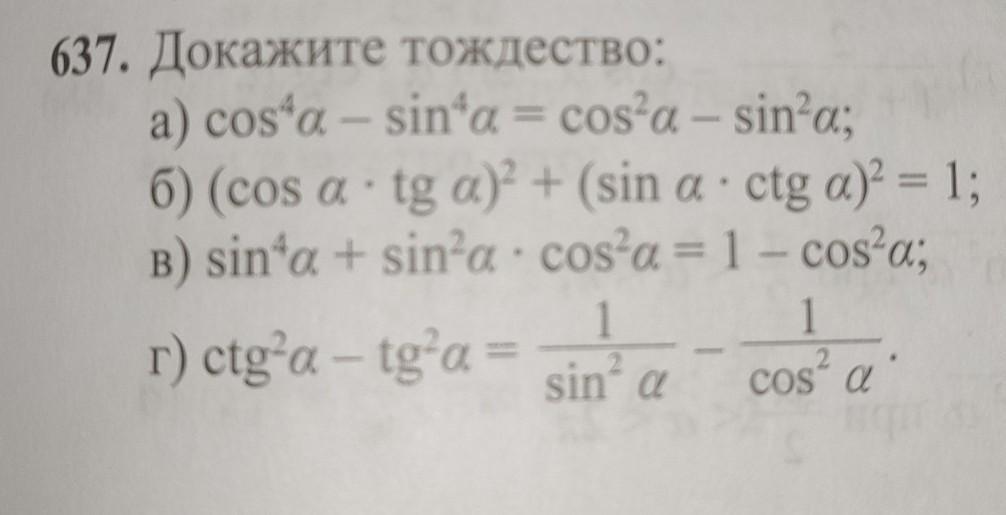
diana99444:
да да да да пожалуйста
а правильно точно?
Ответы
Автор ответа:
3
а остальное????
а нет там все
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: 971097
Предмет: Русский язык,
автор: rawushka
Предмет: Математика,
автор: незабудка123
Предмет: Окружающий мир,
автор: котик1029
Предмет: Қазақ тiлi,
автор: MelisaMarciano