Question

Из точки A, которая лежит вне плоскости a, проведены к этой плоскости наклонные AC и AD, образующие с ней углы 45 и 60 соответственно. Найдите длмну проекции наклонной AD на плоскость a, если AC = 4 корня из 2см

Answer 1

Ответ:

длина проекции наклонной AD на плоскость α равна  $\displaystyle \boldsymbol {\frac{4\sqrt{3} }{3} }$см

Пошаговое объяснение:

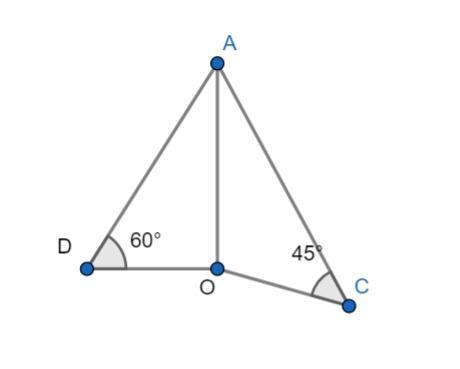
Сделаем чертеж.

Опустим из точки А перпендикуляр на плоскость α.

По чертежу:

ΔАОС - равнобедренный (∠АСО = 45°), следовательно

$\boldsymbol {} \displaystyle 2(AO)^2=(4\sqrt{2}cm )^2\\\\ 2(AO)^2 = (16*2)cm=32cm\\\\AO = 4cm$

AO = 4см

Теперь перейдем к ΔAOD

∠ ADO = 60°    ⇒  ∠DAO = 30°

Обозначим DO = x, тогда DA = 2x (гипотенуза и катет, лежащий против угла в 30°)

Запишем теорему Пифагора для  ΔAOD

(DA)² = (DO)² +(AO)²

(2x)² = x² + 4²

4x² = x² +16

3x² = 16

x² = 16/3

$\displaystyle \boldsymbol {x=\frac{4}{\sqrt{3}} =\frac{4\sqrt{3} }{3} }$  

Таким образом, возвращаясь к нашим обозначениям, мы получим длину проекции  наклонной AD на плоскость α