Предмет: Алгебра,
автор: danilbabenko81
Помогите пожалуйста срочно дам 50 балов
Приложения:
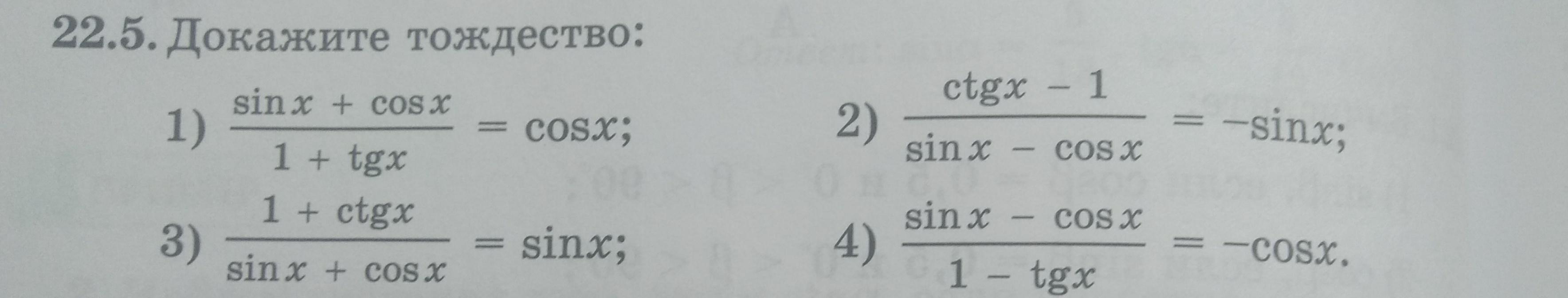
Ответы
Автор ответа:
0
Ответ:
1
2
3
4
В 2 и 3, наверно, ошибка, там невозможно получить синус без дроби
Похожие вопросы
Предмет: Физика,
автор: kolin2714
Предмет: Русский язык,
автор: Kiryanovagi
Предмет: Информатика,
автор: Ксю1488
Предмет: Математика,
автор: zero407