Question

"Площадь треугольника. Урок 2"

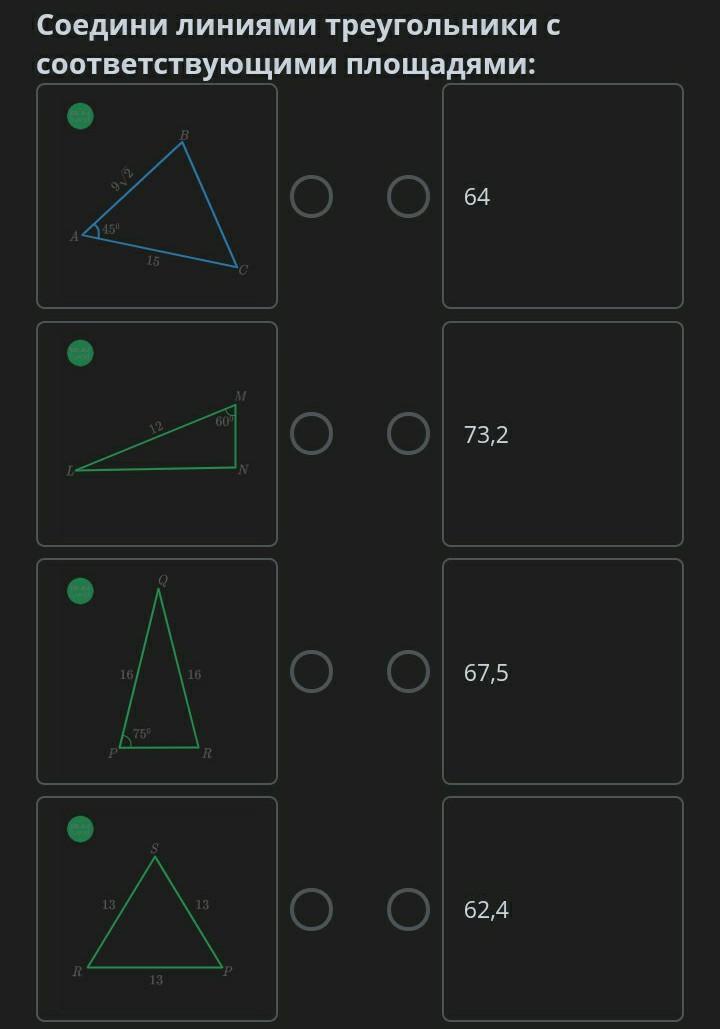
1 - Соедини линиями треугольники с соответствующими площадями:


64

73,2

67,5

62,4
​

Answer 1

Ответ:

1) 67,5

2) 62,4

3) 64

4) 73,2

Объяснение:

1) Площадь треугольника вычисляется, как половина произведения его сторон умноженная на синус угла между ними.

$S = \frac{1}{2} \times AB \times AC \times sin \: a = \frac{1}{2} \times 9 \sqrt{2} \times 15 \times \frac{ \sqrt{2} }{2} = 67.5$

S1=67,5 ед²

2) △LMN(∠N=90°)

По свойству острых углов прямоугольного треугольника ∠L=90°-∠M=90°-60°=30°.

Катет, лежащий напротив угла 30° равен половине гипотенузы: MN= ½ × LM = ½ ×12 = 6

LN=MN×tg60°=6√3

Площадь прямоугольного треугольника равна половине произведения его катетов.

Тогда площадь треугольника будет равна:

$S= \frac{1}{2} \times MN \times LN = \dfrac{12 \times 6 \times \sqrt{3} }{2} = 36 \sqrt{3 } \approx 62.4$

S2=62,4 ед²

3)△PQR - равнобедренный. Следовательно ∠P=∠R=75°. ∠Q=180°-2×75°=30°.

$S = \frac{1}{2} \times PQ \times RQ \times sin30 = \frac{1}{2} \times 16 \times 16 \times \frac{1}{2} = 64$

S3=64 ед²

4) △RSP равносторонний. В равностороннем треугольнике все углы по 60°.

$S = \frac{1}{2} \times RS \times RP \times sin60 = \frac{1}{2} \times 13 \times 13 \times \frac{ \sqrt{3} }{2} = 42.25 \sqrt{3} \approx 73.2$

S4= 73,2 ед²