Предмет: Математика,
автор: lerussia74
Помогите решить пожалуйста
Приложения:
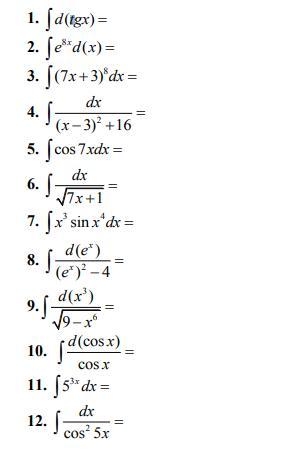
Ответы
Автор ответа:
1
Ответ:
1
2
3
4
5
6
7
8
9
10
11
12
Похожие вопросы
Предмет: Информатика,
автор: bek87
Предмет: Русский язык,
автор: Дурдон
Предмет: Математика,
автор: vitamin77
Предмет: Алгебра,
автор: egormatveev81000
Предмет: Русский язык,
автор: Albina0981