Предмет: Геометрия,
автор: ivannasabadochows5ub
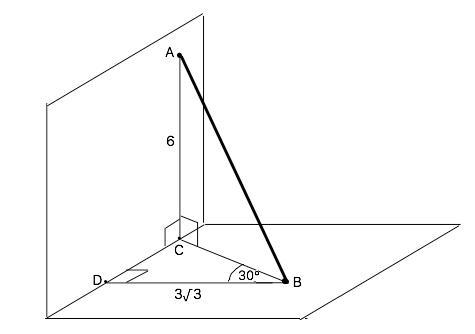
Концы отрезка АВ лежат в перпендикулярных плоскостях. AC и BD - перпендикуляры, проведенные к линии пересечения этих плоскостей, AC = 6 м, BD = 3 корень из 3 м. Найдите длину отрезка АВ, если угол DBC = 30
Кінці відрізка АВ лежать у перпендикулярних площинах. AC і BD - перпендикуляри, проведені до лінії перетину цих площин, AC = 6 м, BD = 3 корінь з 3 м. Знайдіть довжину відрізка АВ, якщо кут DBC=30
Ответы
Автор ответа:
2
Ответ:
AB = 6√2 м
Объяснение:
ivannasabadochows5ub:
в книге пишет ответ 6 корень с 2, но спасибо
извините
там bd должно делиться на косинус, а я умножил
исправил ошибку
Автор ответа:
4
Ответ: 6√2 м
Объяснение: Рассмотрим сделанный согласно условию рисунок. Треугольники АВС и ВCD - прямоугольные.
СВ=ВD:cos30°=3√3:(√3/2)=6 ⇒
∆ АВС - равнобедренный. По т.Пифагора или через синус или косинус угла ( острые углы равнобедренного прямоугольного треугольника равны 45°) АВ=ВС:sin45°=6:(1/√2)=6√2 м.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: totalwar5555
Предмет: Математика,
автор: dmitryboz21
Предмет: Русский язык,
автор: SCamilla
Предмет: Математика,
автор: кириллрешатель