Question

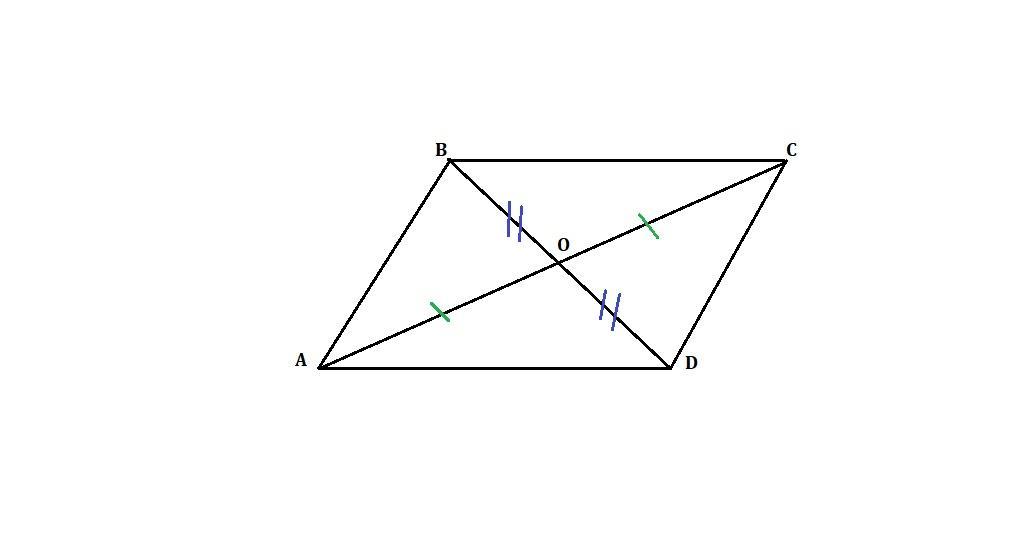
4. Скільки пар рівних трикутників зображе-
но на рисунку?
А) 1;
В) 3;
Б) 2;
Г) 4.,​

Answer 1

Ответ:

Г) 4

Объяснение:

АBCD - четырёхугольник. АС и BD - диагонали, по условию ВО=OD, AO=OC.

• Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

⇒ АBCD - параллелограмм. В параллелограмме противоположные стороны попарно параллельны : АВ║CD, BC ║AD.

Свойство параллелограмма:

В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, ∠ABC = ∠ADC, ∠BAD = ∠BCD

1) ΔAOD и ΔCOВ

∠AOD = ∠COВ - как вертикальные, ВО=OD, AO=OC - по условию,

ΔAOD = ΔCOВ по двум сторонам и углу между ними (1 признак равенства треугольников)

2) ΔAОВ и ΔCOD

∠AOВ = ∠COD - как вертикальные, ВО=OD, AO=OC - по условию,

ΔAОВ = ΔCOD по двум сторонам и углу между ними (1 признак равенства треугольников)

3) ΔABD и  ΔCDВ

AB = CD, BC = AD, ∠BAD = ∠BCD - по свойству параллелограмма, ⇒

ΔABD =  ΔCBD по двум сторонам и углу между ними (1 признак равенства треугольников)

4) ΔABC и ΔADC

AB = CD, BC = AD, ∠ABC = ∠ADC - по свойству параллелограмма, ⇒

ΔABC и ΔADC по двум сторонам и углу между ними (1 признак равенства треугольников).