Предмет: Математика,
автор: Аноним
Решить примеры которые на доске, решить полностью
Приложения:
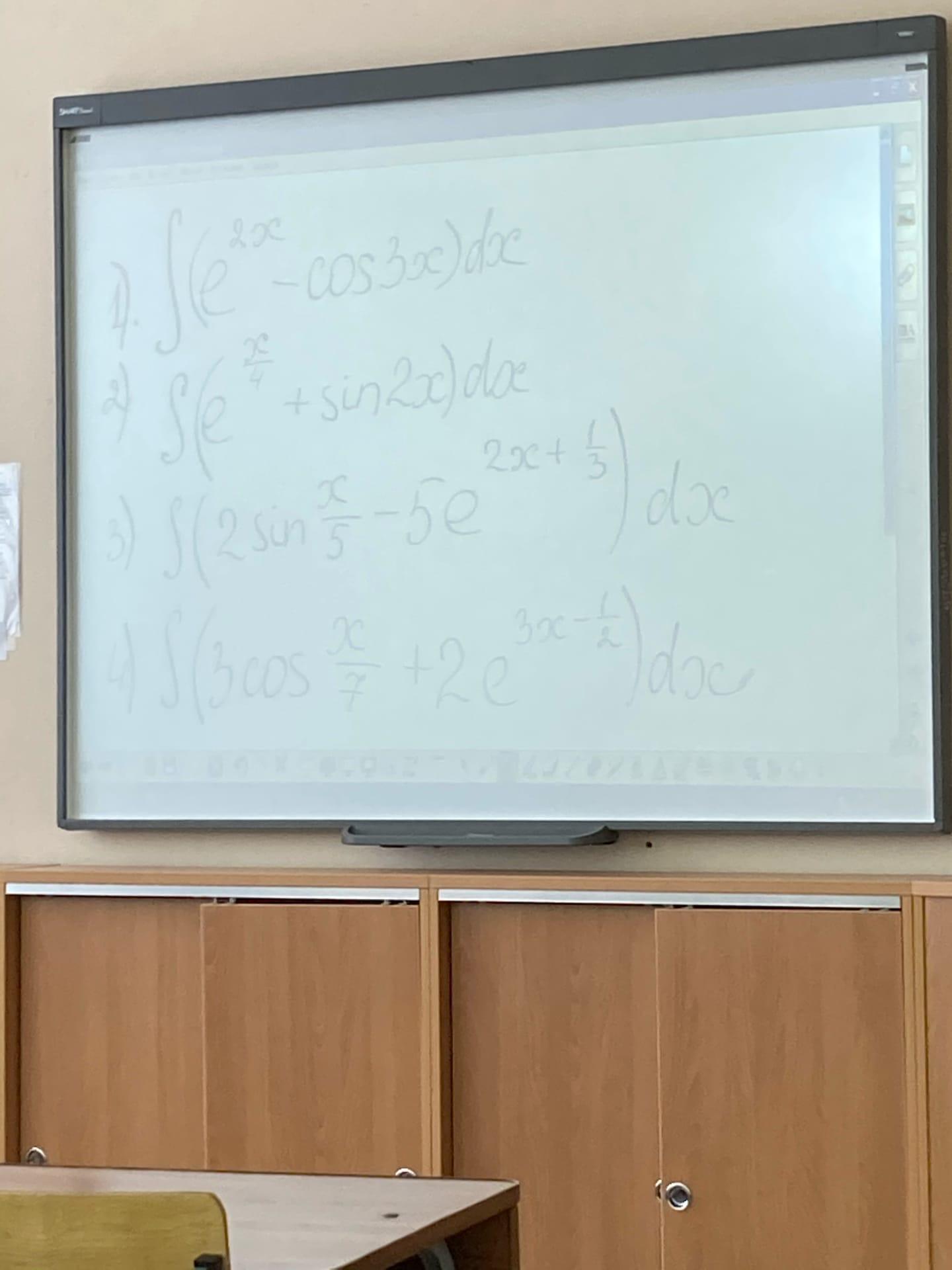
Ответы
Автор ответа:
1
Ответ:
1
2
3
Похожие вопросы
Предмет: Литература,
автор: abdhhdhhh25553
Предмет: Английский язык,
автор: irenefimen
Предмет: Химия,
автор: Lizadenis
Предмет: Русский язык,
автор: Ляпомогите
Предмет: Окружающий мир,
автор: sanzhar220