Предмет: Алгебра,
автор: dosmogombetovaz
помогите пожалуйста
Приложения:
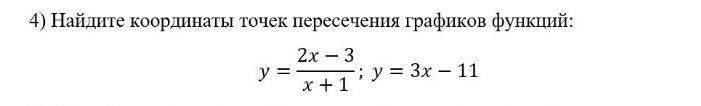
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ:
Решение:
Оба корня удовлетворяют ОДЗ.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Fprlf
Предмет: Геометрия,
автор: forever9
Предмет: Русский язык,
автор: erkebulanartur