Предмет: Алгебра,
автор: spacegrace67
17.9 и 17.10
ПОМОГИТЕ ОЧЕНЬ НУЖНО ДАМ 37 БАЛЛОВ
ТОЛЬКО С РЕШЕНИЕМ ПРОСТО ОТВЕТ НЕ НУЖЕН
Приложения:
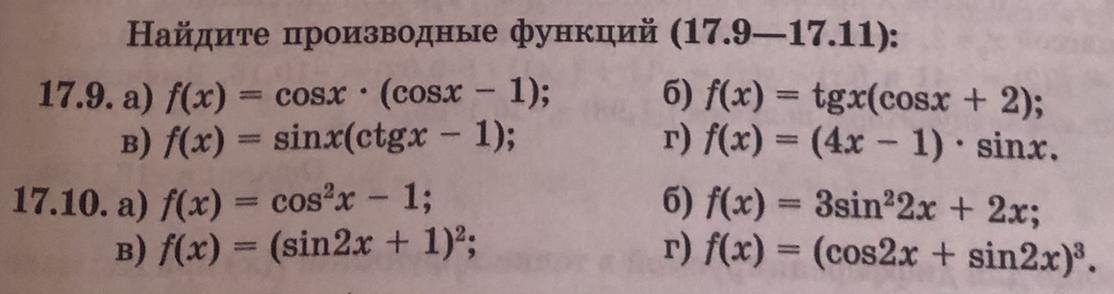
Ответы
Автор ответа:
1
Ответ:
17.9
а)
б)
в)
г)
17.10
а)
б)
в)
г)
spacegrace67:
Спасибо тебе огромное!!!! Ты как всегда лучшая:))))))
привет! Можешь пожалуйста помочь с геометрией у меня в вопросах она есть 22.3, очень нужно
привет! мне очень нужна твоя помощь, можешь пожалуйста у меня в вопросах решить 23.1 , только подробно
Похожие вопросы
Предмет: Физика,
автор: solovey1310
Предмет: Математика,
автор: anisimovaaleks
Предмет: Русский язык,
автор: jurik199702281
Предмет: Математика,
автор: Rais375