Предмет: Алгебра,
автор: smart380
помогите пожалуйста
Приложения:
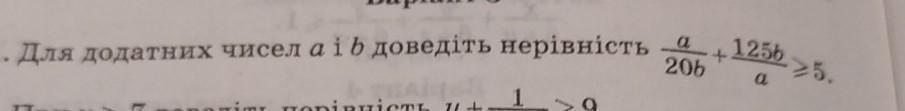
Ответы
Автор ответа:
1
Приводим к общему знаменателю.
Для уточнения. 5 я перенёс через знак со знаком минус и умножил и числитель и знаменатель на 20ab.
Получается раскрытая формула квадрата разницы.
И так. В числителе получается положительное число, ибо любое число в квадрате априори положительное.
В знаменателе же из условия мы получаем произведение положительных.
Положительное делённое на положительное даёт либо ноль либо положительное. Что и требовалось доказать.
Похожие вопросы
Предмет: Русский язык,
автор: ishb
Предмет: Алгебра,
автор: Fakee48
Предмет: Физика,
автор: Acio50
Предмет: Алгебра,
автор: polinapopopo
Предмет: Химия,
автор: Щвфьфигтфпф