Предмет: Математика,
автор: Diana8814
ПОМОГИТЕ ПОЖАЛУЙСТА!!! СРОЧНО!
Найти первую производную функции
Приложения:
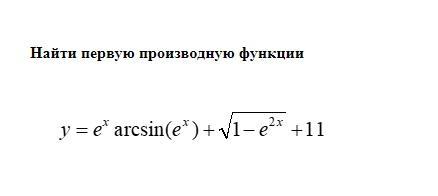
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1.
2.
3.
(11)' = 0
итого ответ
Похожие вопросы
Предмет: Математика,
автор: imerenyuk
Предмет: Русский язык,
автор: enkhzaya
Предмет: Русский язык,
автор: viktorolya
Предмет: Математика,
автор: Вврвара23367
Предмет: Алгебра,
автор: NikitaxDxd